18 分钟
机器学习实战(Peter Harrington)阅读笔记(一)
一、机器学习基础
略
二、k-近邻算法
1、k-近邻算法概述
简单地说,k-近邻算法采用测量不同特征值之间的距离方法进行分类。
(1)优缺点
- 优点:精度高、对异常值不敏感、无数据输入假定。
- 缺点:计算复杂度高、空间复杂度高。
- 适用数据范围:数值型和标称型。
(2)工作原理
存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
这个算法不需要训练模型,在执行过程中输入与每个样本计算计算距离,然后选取最小的k个样本,其中出现最多的类别为这个输入的类别
(3)一般流程
- 收集数据:可以使用任何方法。
- 准备数据:距离计算所需要的数值,最好是结构化的数据格式。
- 分析数据:可以使用任何方法。
- 训练算法:此步骤不适用于k-近邻算法。
- 测试算法:计算错误率。
- 使用算法:首先需要输入样本数据和结构化的输出结果,然后运行k-近邻算法判定输入数据分别属于哪个分类,最后应用对计算出的分类执行后续的处理。
(4)编程实现
创建数据
from numpy import *
def createDataSet():
group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
labels = ['A','A','B','B']
return group, labelsk-近邻算法
def kNN(X, dataSet, labels, k):
"""
X: 要分类的样本
dataSet: 数据集
labels:标签
k:k最邻近算法的参数
"""
m, n = dataSet.shape #样本数目和特征数
# 计算样本与数据集之间的距离,采用欧拉距离
d = np.sum( (np.tile(X,(m,1)) - dataSet)**2,1)**0.5
# 对距离进行排序
d = d.argsort()
print(d)
#对类别出现频次进行技术
classCount={}
for i in range(k):
l = labels[d[i]]
classCount[l] = classCount.get(l,0) + 1
return sorted(classCount.items(),
key = lambda asd:asd[1],
reverse=True)[0][0]2、示例:使用 k-近邻算法改进约会网站的配对效果
(0)需求
标签:
- 不喜欢的人
- 魅力一般的人
- 极具魅力的人
特征:
- 每年获得的飞行常客里程数
- 玩视频游戏所耗时间百分比
- 每周消费的冰淇淋公升数
(1)流程
- 收集数据:提供文本文件。
- 准备数据:使用Python解析文本文件。
- 分析数据:使用Matplotlib画二维扩散图。
- 训练算法:此步骤不适用于k-近邻算法。
- 测试算法:使用海伦提供的部分数据作为测试样本。测试样本和非测试样本的区别在于:测试样本是已经完成分类的数据,如果预测分类与实际类别不同,则标记为一个错误。
- 使用算法:产生简单的命令行程序,然后海伦可以输入一些特征数据以判断对方是否为自己喜欢的类型。
(2)读取数据
def file2matrix(filename):
"""将文件转化为训练样本矩阵和标签向量X、y"""
fr = open(filename)
lines = fr.readlines() #打开读取文件
X = np.zeros((len(lines), 3)) #初始化样本矩阵和标签向量
y = []
for idx, line in enumerate(lines): #解析填充数据
line = line.strip()
xy = line.split('\t')
X[idx,:] = xy[0:3]
y.append(xy[-1])
return X, np.array(y)(3)分析数据
绘制散点图
import matplotlib
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
# ax.scatter(X[:,1], X[:,2])
ax.scatter(X[:,1], X[:,2], 15.0*y, 15.0*y)
plt.xlabel('Percentage of Time Spent Playing Video Games')
plt.ylabel('Liters of Ice Cream Consumed Per Week')
plt.show()(4)准备数据:归一化数值
下面的公式可以将任意取值范围的特征值转化为0到1区间内的值:
newValue = (oldValue-min)/(max-min)
def autoNorm(X):
"""归一化特征值:newValue = (oldValue-min)/(max-min)"""
minV = X.min(0)
maxV = X.max(0)
ranges = maxV - minV
normX = np.zeros(X.shape)
m = X.shape[0]
normX = (X -minV) / ranges
return normX, ranges, minV(5)测试算法
def datingClassTest():
X,y = file2matrix('datingTestSet2.txt') #从文件中加载数据集
normX, ranges, minV = autoNorm(X)
m = normX.shape[0] # 样本数目
tlen = int(m*0.1) # 测试集长度test length
errCnt = 0
for i in range(tlen):
res = kNN(normX[i,:],normX[tlen:m,:],y[tlen:m],3)
print ("分类器返回: %d, 正确答案是: %d" % (res, y[i]))
if (res != y[i]): errCnt += 1
print ("错误率为: %f" % (errCnt/tlen))
print (errCnt)(6)使用算法:构建完整可用系统
def classifyPerson():
resultList = ['一点也不', '有一点', '非常喜欢']
percentTats = float(input(\
"玩视频游戏所耗时间百分比?"))
ffMiles = float(input("每年获得的飞行常客里程数?"))
iceCream = float(input("每周消费的冰淇淋公升数?"))
datingDataMat, datingLabels = file2matrix('datingTestSet2.txt')
normMat, ranges, minVals = autoNorm(datingDataMat)
inArr = np.array([ffMiles, percentTats, iceCream, ])
classifierResult = kNN((inArr - \
minVals)/ranges, normMat, datingLabels, 3)
print ("你将可能喜欢这个人: %s" % resultList[classifierResult - 1])3、示例:使用kNN进行手写识别系统
def img2vector(filename):
"""读取图片"""
returnVect = np.zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0,32*i+j] = int(lineStr[j])
return returnVect
def handwritingClassTest():
"""使用kNN算法对手写数字进行分类"""
hwLabels = []
trainingFileList = os.listdir('trainingDigits') #加载训练集
m = len(trainingFileList)
trainingMat = np.zeros((m,1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0] #take off .txt
classNumStr = int(fileStr.split('_')[0])
hwLabels.append(classNumStr)
trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr)
testFileList = os.listdir('testDigits') #iterate through the test set
errorCount = 0.0
mTest = len(testFileList)
for i in range(mTest):
fileNameStr = testFileList[i]
fileStr = fileNameStr.split('.')[0] #take off .txt
classNumStr = int(fileStr.split('_')[0])
vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
classifierResult = kNN(vectorUnderTest, trainingMat, hwLabels, 3)
print ("分类器返回: %d, 真正的答案: %d" % (classifierResult, classNumStr))
if (classifierResult != classNumStr): errorCount += 1.0
print ("\n出错总数: %d" % errorCount)
print ("\n错误率: %f" % (errorCount/float(mTest)))三、决策树
1、决策树概述
(1)优缺点
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。 缺点:可能会产生过度匹配问题。 适用数据类型:数值型和标称型。
(2)伪代码
createBranch():
If so return 类标签;
Else
寻找划分数据集的最好特征
划分数据集
创建分支节点
for 每个划分的子集
调用函数createBranch并增加返回结果到分支节点中
return 分支节点(3)一般流程
- 收集数据:可以使用任何方法。
- 准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化。
- 分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期。
- 训练算法:构造树的数据结构。
- 测试算法:使用经验树计算错误率。
- 使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
(4)ID3算法简介
2、信息论相关知识
(1)信息熵(entropy)
\( X = {x_1, x_2,…, x_n} \) 是事件\(x_i(i=1,2,…,n)\)的集合,\(p(x_i)\)表示事件\(x\)发生的概率。 那么信息熵\(H(X)\)表达式为: $$ H(X) = - \sum_{i=1}^{n} p(x_i) \log p(x_i) $$
信息熵(entropy)描述的是信息不确定性的度量,熵越大表示信息的不确定性越大,信息量越大
(2)信息增益
在划分数据集之前之后信息发生的变化称为信息增益,知道如何计算信息增益,我们就可以计算每个特征值划分数据集获得的信息增益,获得信息增益最高的特征就是最好的选择。
信息增益\(I(X,Y)\)公式(表示X集合经过Y划分): $$ I(X,Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) $$ 条件概率公式 $$ P(A|B) = \frac{P(AB)}{ P(B)} $$
H(Y|X)表示经过划分后各个子集的 信息熵*(子集占比) 的和,也就是说子集的信息熵的加权和
理解:为何要选择I(X,Y)大的
- H(X)不变,若I(X,Y)越大,则H(Y|X)越小
- H(Y|X)越小,表示子集的不确定性越小,从而降低了决策树的不确定性
3、决策树实现
(1)计算信息熵
def entropy(y):
"""计算信息熵"""
m = y.shape[0]
yCnt = {}
for l in y:
yCnt[l] = yCnt.get(l, 0) + 1
ret = 0.0
for k in yCnt:
p = yCnt[k] / m
ret -= p * math.log(p,2)
return ret创建测试数据
def createDataSet():
"""创建测试数据"""
X = np.array([[1, 1],
[1, 1],
[1, 0],
[0, 1],
[0, 1]])
y = np.array(['yes','yes','no','no','no'])
featNames = ['no surfacing','flippers'] #各个特征的成员名字
return X,y,featNames(2)划分数据集
def splitDataSet(X, y, axis, value):
"""分割数据集,去除axis轴的特征,
选取该特征为value的样本"""
retDataSet = []
retX, rety = [], []
for i, x in enumerate(X):
if x[axis] == value: # 选择符合要求的样本
retX.append(np.append(x[:axis],x[axis+1:]))
rety.append(y[i])
return np.array(retX),np.array(rety)(3)计算每个划分信息增益选择最佳划分
def bestSplit(X,y):
"""选择最好的划分,返回最好的划分的特征序号"""
m, n = X.shape
baseEntropy = entropy(y)
bestFeature = -1 #特征序号初始化为-1
bestInfoGain = 0.0 #最好的信息增益初始化为0.0
for i in range(n):
featSet = set(X[:,i])
newEntropy = 0.0
for val in featSet: #计算条件熵
subX, suby = splitDataSet(X,y,i,val)
p = subX.shape[0] / m
newEntropy += p*entropy(suby)
infoGain = baseEntropy - newEntropy #计算信息增益
if(infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature(4)递归创建决策树
def createDTree(X,y,featNames=None):
"""递归构建决策树
featName: python数组类型,长度为n,特征名列表"""
if(featNames == None):
featNames = ["feature%d"%i for i in range(X.shape[1])]
if(np.sum(y == y[0]) == len(y)): # 类别完全相同则停止继续划分
return y[0]
if(X.shape[1] == 0): # 没有可以划分的特征
return Counter(y).most_common()[0] #返回
bestFeat = bestSplit(X,y) #最优划分的特征序号
bestFeatName = featNames[bestFeat] #最优划分的特征名
dtree = {bestFeatName:{}}
#del(featNames[bestFeat]) #从参数列表中删除
featSet = set(X[:,bestFeat]) #获取该特征的所有取值
for val in featSet: #构造子节点
subFeatNames = featNames[:bestFeat] + featNames[bestFeat+1:]
dtree[bestFeatName][val] = createDTree(
*splitDataSet(X,y,bestFeat,val),
subFeatNames)
return dtree(5)对新的输入进行分类
def classify(dtree,x, featNames = None):
"""分类器"""
if(featNames == None):
featNames = ["feature%d"%i for i in range(X.shape[1])]
featName = list(dtree.keys())[0] #获取特征名
subTree = dtree[featName] #获取子树
featIdx = featNames.index(featName) #获取当前特征名在x的索引位置
for key in subTree.keys():
if(x[featIdx] == key):
if(type(subTree[key]).__name__=='dict'):
y = classify(subTree[key],x,featNames)
else: y = subTree[key]
return y(6)持久化和加载
def saveDTree(dtree,filename):
"""持久化树"""
import pickle
fw = open(filename,'w')
pickle.dump(inputTree,fw)
fw.close()
def loadDTree(filename):
"""加载树"""
import pickle
fr = open(filename)
return pickle.load(fr)4、示例:使用决策树预测隐形眼镜类型
fr = open('lenses.txt')
lenses = np.array([ l.strip().split('\t') for l in fr.readlines()])
X, y = lenses[:,0:-1], lenses[:,-1]
featNames = ['age', 'prescript', 'astigmatic', 'tearRate']
lensesTree = dtree.createDTree(X,y,featNames)
print(lensesTree)
treePlotter.createPlot(lensesTree)四、朴素贝叶斯
1、条件概率
公式一 $$ p(y|x) = \frac{p(xy)}{p(x)} $$ 公式二 $$ p(y|x) = \frac{p(x|y)p(y)}{p(x)} $$
2、使用条件概率来分类
$$ \max p(y_i|x) = \frac{p(x|y_i)p(y_i)}{p(x)} $$ 因为分母对于所有类别都是常数,所以只要计算分子 $$ \max p(x|y_i)p(y_i) $$ 又因为各特征属性是条件独立的,所以有: $$ p(x|y_i)p(y_i) = p(x^{(0)}|y_i)p(x^{(1)}|y_i)…p(x^{(n)}|y_i)p(y_i) $$ 进一步优化,因为\(p(x^{(n)}|y_i)p(y_i)\)数值非常小,相乘可能造成下溢出所以使用log进行放大
3、朴素贝叶斯分类器实现
(1)从文本中构建词向量
根据文本中的单词在字典中是否出现构建0、1向量
import numpy as np
from collections import Counter
def loadDataSet():
"""创建了一些实验样本。
第一个变量是进行词条切分后的文档集合,
第二个变量是一个类别标签的集合"""
postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
y = np.array([0,1,0,1,0,1]) #1 侮辱性词汇, 0 没有
return postingList, y
def createVocabList(dataSet):
"""返回词典向量"""
vocabSet = set() #创建一个空集
for document in dataSet:
vocabSet = vocabSet | set(document) # 求并集
return list(vocabSet)
def words2Vec(vocabList, words):
"""将词汇列表转换为0,1向量"""
returnVec = [0]*len(vocabList)
for word in words:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else: print ("单词: %s 不在我的词汇表中!" % word)
return np.array(returnVec)
def words2Mat(vocabList, dataSet):
return np.array([words2Vec(vocabList, words) for words in dataSet])(2)训练算法:从词向量计算概率
def trainNB(X,y):
"""计算概率的一些项,返回:
(p(x|y), p(y), 标签名)"""
m, n = X.shape
_y = Counter(y)
for k in _y: _y[k] /= m
p_y = np.array(list(_y.values())) # 计算p(y)
labelNames = list(_y.keys()) # 对应多个的标签名
p_x_y = np.zeros([len(labelNames), n])# 初始化p(x|y)
for idx, l in enumerate(labelNames):
subX = X[y==l]
p_x_y[idx, :] += np.log((subX.sum(0) + 1)/ (subX.sum()+2.0))
return p_x_y, p_y, labelNames(3)分类器
def classifyNB(x,p_x_y,p_y,labelNames):
return labelNames[np.argmax(np.dot(p_x_y,x))](4)测试算法
def testingNB():
dataSet, y = loadDataSet()
vocabList = createVocabList(dataSet)
X = words2Mat(vocabList, dataSet)
p_x_y, p_y, labelNames = trainNB(X,y)
testEntry = ['love', 'my', 'dalmation']
thisDoc = np.array(words2Vec(vocabList, testEntry))
print (testEntry,'被分为: ',classifyNB(thisDoc,p_x_y,p_y,labelNames))
testEntry = ['stupid', 'garbage']
thisDoc = np.array(words2Vec(vocabList, testEntry))
print (testEntry,'被分为: ',classifyNB(thisDoc,p_x_y,p_y,labelNames))(5)朴素贝叶斯词袋模型
def bagOfWords2Vec(vocabList, words):
returnVec = [0]*len(vocabList)
for word in words:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
return np.array(returnVec)
def bagOfWords2Mat(vocabList, dataSet):
return np.array([bagOfWords2Vec(vocabList, words) for words in dataSet])4、示例:使用朴素贝叶斯过滤垃圾邮件
(1)准备数据:切分文本
def textParse(bigString): #input is big string, #output is word list
import re
listOfTokens = re.split(r'\W*', bigString)
return [tok.lower() for tok in listOfTokens if len(tok) > 2](2)测试算法:使用朴素贝叶斯进行交叉验证
def spamTest():
docList=[]; classList = []; fullText =[]
for i in range(1,26):
wordList = textParse(open('email/spam/%d.txt' % i).read())
docList.append(wordList)
fullText.extend(wordList)
classList.append(1)
wordList = textParse(open('email/ham/%d.txt' % i).read())
docList.append(wordList)
fullText.extend(wordList)
classList.append(0)
vocabList = createVocabList(docList)#create vocabulary
trainingSet = list(range(50)); testSet=[] #create test set
for i in range(10):
randIndex = int(np.random.uniform(0,len(trainingSet)))
testSet.append(trainingSet[randIndex])
del(trainingSet[randIndex])
trainMat=[]; trainClasses = []
for docIndex in trainingSet:#train the classifier (get probs) trainNB0
trainMat.append(bagOfWords2Vec(vocabList, docList[docIndex]))
trainClasses.append(classList[docIndex])
p_x_y, p_y, labelNames = trainNB(np.array(trainMat),np.array(trainClasses))
errorCount = 0
for docIndex in testSet: #classify the remaining items
wordVector = bagOfWords2Vec(vocabList, docList[docIndex])
if classifyNB(wordVector, p_x_y, p_y, labelNames) != classList[docIndex]:
errorCount += 1
print ("分类错误邮件为:",docList[docIndex])
print ('错误率为: ',float(errorCount)/len(testSet))
# return vocabList,fullText5、示例:使用朴素贝叶斯分类器从个人广告中获取区域倾向
(1)注意点
- 去除停用词(一些辅助用词):该词表称为停用词表(stop word list),目前可以找到许多停用词表(在本书写作期间,http://www.ranks.nl/resources/stopwords.html 上有一个很好的多语言停用词列表)。
- 输出两个类别的高频词汇:对\(p_x_y\)进行排序选取最大的几个
(2)其他
略
五、逻辑回归
1、编程实现
参见吴恩达课程
class LogisticRegression:
def __init__(self):
pass
def fit(self, X, y, alpha=0.001, epochs=500):
X = np.column_stack((np.ones(X.shape[0]),X))
y = y.reshape((y.shape[0],1))
m, n = np.shape(X)
self.W = np.ones((n,1))
for k in range(epochs): #heavy on matrix operations
h = sigmoid(np.matmul(X, self.W)) #matrix mult
error = (y - h) #vector subtraction
self.W = self.W + alpha * np.matmul(error.transpose(), X).transpose() #matrix mult
def fit1(self, X, y, epochs=150):
X = np.column_stack((np.ones(X.shape[0]),X))
m, n = np.shape(X)
self.W = np.ones(n) #initialize to all ones
for j in range(epochs):
dataIndex = list(range(m))
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
randIndex = int(np.random.uniform(0,len(dataIndex)))#go to 0 because of the constant
h = sigmoid(np.sum(X[randIndex]*self.W))
error = y[randIndex] - h
self.W = self.W + alpha * error * X[randIndex]
del(dataIndex[randIndex])
self.W = self.W[:,np.newaxis]
def predict(self, x):
x = np.array(x)
if(x.ndim == 1): x = x[np.newaxis,:]
x = np.column_stack((np.ones(x.shape[0]),x))
p = sigmoid(np.matmul(x,self.W))
return p > 0.5六、SVM
略
七、利用AdaBoost元算法提高分类性能
1、基于数据集多重抽样的分类器
(1)bagging:基于数据随机重抽样的分类器构建方法
自举汇聚法(bootstrap aggregating),也称为bagging方法,是在从原始数据集选择S次后得到S个新数据集的一种技术
在S个数据集建好之后,将某个学习算法分别作用于每个数据集就得到了S个分类器。当我们要对新数据进行分类时,就可以应用这S个分类器进行分类。与此同时,选择分类器投票结果中最多的类别作为最后的分类结果。
当然,还有一些更先进的bagging方法,比如随机森林(random forest)。
(2)boosting
boosting是一种与bagging很类似的技术。不论是在boosting还是bagging当中,所使用的多个分类器的类型都是一致的。但是在前者当中,不同的分类器是通过串行训练而获得的,每个新分类器都根据已训练出的分类器的性能来进行训练。boosting是通过集中关注被已有分类器错分的那些数据来获得新的分类器。
2、AdaBoost算法原理
(1)AdaBoost的一般流程
- 收集数据:可以使用任意方法。
- 准备数据:依赖于所使用的弱分类器类型,本章使用的是单层决策树,这种分类器可以处理任何数据类型。当然也可以使用任意分类器作为弱分类器,第2章到第6章中的任一分类器都可以充当弱分类器。作为弱分类器,简单分类器的效果更好。
- 分析数据:可以使用任意方法。
- 训练算法:AdaBoost的大部分时间都用在训练上,分类器将多次在同一数据集上训练弱分类器。
- 测试算法:计算分类的错误率。
- 使用算法:同SVM一样,AdaBoost预测两个类别中的一个。如果想把它应用到多个类 别的场合,那么就要像多类SVM中的做法一样对AdaBoost进行修改。
(2)几个公式
错误率 $$ \epsilon = \frac{为正确分类的样本}{所有样本} $$ alpha每个弱分类器的权值 $$ \alpha = frac{1}{2}\ln(\frac{1-\epsilon}{\epsilon}) $$
(3)AdaBoost图解
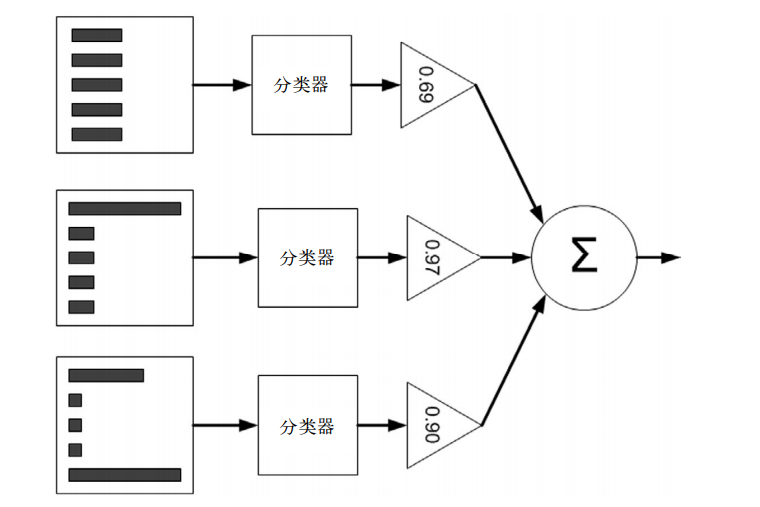
- 其中直方图的不同宽度表示每个样例上的不同权重D。
- 在经过一个分类器之后,加权的预测结果会通过三角形中的alpha值进行加权。
- 每个三角形中输出的加权结果在圆形中求和,从而得到最终的输出结果
- 下一层的D是根据上一层的D和alpha计算得来的
- 每一层是一个迭代的一步
计算出alpha值之后,可以对权重向量D进行更新,以使得那些正确分类的样本的权重降低而错分样本的权重升高。D的计算方法如下。 如果某个样本被正确分类,那么该样本的权重更改为: $$ D^{(t+1)}_i = \frac{D^{(t)}_t e^{-\alpha}}{\sum_i D_i} $$ 而如果某个样本被错分,那么该样本的权重更改为: $$ D^{(t+1)}_i = \frac{D^{(t)}_t e^{\alpha}}{\sum_i D_i} $$
3、AdaBoost编程实现
class AdaBoost:
def __init__(self):
pass
def __stumpClassify(self, X,featIdx,threshVal,threshIneq):
"""单层决策树对一组数据进行分类
参数说明:(X, 特征下标,边界值,正类的选择)"""
retArray = np.ones((np.shape(X)[0],1)) #shape(m,1)
if threshIneq == 'lt':
retArray[X[:,featIdx] <= threshVal] = -1.0
else:
retArray[X[:,featIdx] > threshVal] = -1.0
return retArray
def __buildStump(self, X, y, D):
"""构建最佳的单层决策树"""
m, n = np.shape(X)
numSteps = 10.0 #划分数据边界的分割步数
bestStump = {} #记录单层决策树的结构
bestClasEst = np.mat(np.zeros((m,1))) #纪录决策树的预测值
minError = np.inf #初始化误差和为正无穷
for i in range(n): # 遍历所有特征
rangeMin = X[:,i].min() #获取该特征的上下界
rangeMax = X[:,i].max()
stepSize = (rangeMax-rangeMin)/numSteps
for j in range(-1,int(numSteps)+1):# 遍历所有换分
for inequal in ['lt', 'gt']: #决定哪个为正类
threshVal = (rangeMin + float(j) * stepSize) #边界值
predictedVals = self.__stumpClassify(X,i,threshVal,inequal)#call stump classify with i, j, lessThan
errArr = np.ones((m,1)) #shape(m,1)
errArr[predictedVals == y] = 0
weightedError = np.matmul(D.T, errArr) #对不同的样本给予不同的权重
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i #划痕的特征下表达式
bestStump['thresh'] = threshVal #边界值
bestStump['ineq'] = inequal #大于还是下雨边界值的为正类
return bestStump,minError,bestClasEst
def fit(self, X, y, numIt=40):
"""X:np.array类型,数据可以为连续的
y:python list类型,二元取值,-1.0或者1.0"""
y = np.array(y)
y = y.reshape((y.shape[0], 1))
weakClassArr = [] #弱分类器列表
m = np.shape(X)[0]
D = np.ones((m,1))/m #初始化D为等概率
aggClassEst = np.zeros((m,1))
for i in range(3):
# 构建一个决策树
bestStump,error,classEst = self.__buildStump(X,y,D)
#print ("D:",D.T)
# 计算alpha
alpha = float(0.5*np.log((1.0-error)/max(error,1e-16)))
bestStump['alpha'] = alpha # 每个分类器的权重
#储存决策树
weakClassArr.append(bestStump)
#print ("classEst: ",classEst.T)
expon = np.multiply(-1*alpha*y,classEst) #exponent for D calc, getting messy
# 为下一次迭代更新D
D = np.multiply(D,np.exp(expon))
D = D/D.sum()
#calc training error of all classifiers, if this is 0 quit for loop early (use break)
aggClassEst += alpha*classEst #对分类器的结果进行加权求和
#print ("aggClassEst: ",aggClassEst.T)
#获得最终结果
aggErrors = np.multiply(np.sign(aggClassEst) != y, np.ones((m,1)))
errorRate = aggErrors.sum()/m
print ("total error: ",errorRate)
if errorRate == 0.0: break
self.weakClassArr = weakClassArr
def predict(self,x):
classifierArr = self.weakClassArr
dataMatrix = np.mat(x).A #do stuff similar to last aggClassEst in adaBoostTrainDS
m = np.shape(dataMatrix)[0]
aggClassEst = np.zeros((m,1))
for i in range(len(classifierArr)):
classEst = self.__stumpClassify(dataMatrix, classifierArr[i]['dim'],\
classifierArr[i]['thresh'],\
classifierArr[i]['ineq'])#call stump classify
aggClassEst += classifierArr[i]['alpha']*classEst
print (aggClassEst)
return np.sign(aggClassEst)4、分类性能指标
参见 偏斜类
八、预测数值型数据:回归
符号说明
- w表示权重
- \(\hat{w}\) w的一个最佳估计
1、普通最小二乘法
$$ \hat{w} = (X^TX)^(-1)X^Ty $$
def standRegres(X,y):
"""标准线性回归(普通最小二乘法)
公式:\hat{w} = (X^TX)^(-1)X^Ty
"""
X = np.mat(X); y = np.mat(y).T
xTx = X.T*X
if np.linalg.det(xTx) == 0.0:
print("This matrix is singular, cannot do inverse")
return
ws = xTx.I * (X.T*y)
return ws2、局部加权线性回归
$$ \hat{w} = (X^TWX)^(-1)X^TWy $$ 其中W是一个m*m的对角含元素的矩阵 $$ w(i, i) = exp(\frac{|x^{(i)}-x|}{-2k^2}) $$
其中k是用户需要制定的参数
- k 越大结果与线性回归越接近
k 越小可能出现过拟合
def lwlr(testPoint,X ,y ,k=1.0): """局部加权线性回归函数 \hat{w} = (X^TWX)^(-1)X^TWy W是一个对角矩阵其中,是一个核函数 w(i, i) = exp(\frac{|x^{(i)}-x|}{-2k^2}) """ xMat = np.mat(X); yMat = np.mat(y).T m = np.shape(xMat)[0] weights = np.mat(np.eye((m))) for j in range(m): #next 2 lines create weights matrix diffMat = testPoint - xMat[j,:] # weights[j,j] = np.exp(diffMat*diffMat.T/(-2.0*k**2)) xTx = xMat.T * (weights * xMat) if np.linalg.det(xTx) == 0.0: print ("This matrix is singular, cannot do inverse") return ws = xTx.I * (xMat.T * (weights * yMat)) return testPoint * ws
3、岭回归
$$ \hat{w} = (X^TX + \lambda I)^{-1}X^{T}y $$
- λ是一个用户定义的数值
I代码是m的单位矩阵
def ridgeRegres(xMat,yMat,lam=0.2): """岭回归: \hat{w} = (X^TX + \lambda I)^{-1}X^{T}y """ xTx = xMat.T*xMat denom = xTx + np.eye(np.shape(xMat)[1])*lam if np.linalg.det(denom) == 0.0: print ("This matrix is singular, cannot do inverse") return ws = denom.I * (xMat.T*yMat) return ws
4、lasso和前向逐步回归
数据标准化,使其分布满足0均值和单位方差
在每轮迭代过程中:
设置当前最小误差lowestError为正无穷
对每个特征:
增大或缩小:
改变一个系数得到一个新的W
计算新W下的误差
如果误差Error小于当前最小误差lowestError:设置Wbest等于当前的W
将W设置为新的Wbest这是一种贪心算法,首先初始化权重W为1,然后针对每个特征的权重增加或减小一个很小的值,误差若减小,更新权重。一次往复直至趋于稳定
def regularize(xMat):#数据标准化
inMat = xMat.copy()
inMeans = np.mean(inMat,0) #calc mean then subtract it off
inVar = np.var(inMat,0) #calc variance of Xi then divide by it
inMat = (inMat - inMeans)/inVar
return inMat
def rssError(yArr,yHatArr): #yArr and yHatArr both need to be arrays
return ((yArr-yHatArr)**2).sum()
def stageWise(xArr,yArr,eps=0.01,numIt=100):
xMat = np.mat(xArr); yMat=np.mat(yArr).T
yMean = np.mean(yMat,0)
yMat = yMat - yMean #can also regularize ys but will get smaller coef
xMat = regularize(xMat)
m,n=np.shape(xMat)
returnMat = np.zeros((numIt,n)) #testing code remove
ws = np.zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()
for i in range(numIt):
lowestError = np.inf;
for j in range(n):
for sign in [-1,1]:
wsTest = ws.copy()
wsTest[j] += eps*sign
yTest = xMat*wsTest
rssE = rssError(yMat.A,yTest.A)
if rssE < lowestError:
lowestError = rssE
wsMax = wsTest
ws = wsMax.copy()
returnMat[i,:]=ws.T
return returnMat5、权衡偏差与方差
参见:算法的高偏差与高方差
九、树回归
1、回归树
回归树类似于决策树,不同点在于划分的方式
- 决策树划分是根据选定一个特征的情况的计算信息熵
回归树划分是根据选定一个特征和边界计算数据集的总方差
import numpy as np def loadDataSet(fileName): dataMat = [] fr = open(fileName) for line in fr.readlines(): curLine = line.strip().split('\t') fltLine = list(map(float,curLine)) #map all elements to float() dataMat.append(fltLine) return np.mat(dataMat) def binSplitDataSet(dataSet, feature, value): """对数据按照行进行二元分割""" mat0 = dataSet[np.nonzero(dataSet[:,feature] > value)[0],:] mat1 = dataSet[np.nonzero(dataSet[:,feature] <= value)[0],:] return mat0,mat1 def regLeaf(dataSet): """计算叶子节点的值,就是这一部分数据集标签的均值""" return np.mean(dataSet[:,-1]) def regErr(dataSet): """计算数据集的总方差 = 方差*m""" return np.var(dataSet[:,-1]) * np.shape(dataSet)[0] def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)): """ 选择数据集的最好划分,最优的划分意味着:样本标签的总方差小 """ tolS = ops[0]; tolN = ops[1] #if all the target variables are the same value: quit and return value # 如果所有的样本的标签一致,则直接返回为叶子节点 if len(set(dataSet[:,-1].T.tolist()[0])) == 1: #exit cond 1 return None, leafType(dataSet) m, n = np.shape(dataSet) #计算整个样本集的总方差 S = errType(dataSet) # 循环划分数据集重新计算误差,找到最小的划分方案 bestS = np.inf; bestIndex = 0; bestValue = 0 for featIndex in range(n-1): #遍历所有特征 for splitVal in set(dataSet[:,featIndex].T.tolist()[0]): #遍历所有的划分值 # 执行划分 mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal) # 划分后的样本数目要大于等用户设定的参数 if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue newS = errType(mat0) + errType(mat1) #计算总方差 if newS < bestS: #更新划分方案 bestIndex = featIndex bestValue = splitVal bestS = newS # 如果划分后误差的减小没有达到用户设定的值,则返回为叶子节点 if (S - bestS) < tolS: return None, leafType(dataSet) #exit cond 2 #如果划分后的两个数据集合的样本数目存在一个小于用户设定值,则返回叶子节点 mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue) if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): #exit cond 3 return None, leafType(dataSet) return bestIndex,bestValue #返回为非叶子节点的划分 def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)): """ dataSet包含特征和表亲啊 X=dataSet[:,0:-1],y=dataSet[:,-1] leafType是对创建叶节点的函数的引用 errType计算误差的函数引用 ops是一个用户定义的参数构成的元组,用以完成树的构建。 用作预剪枝 [0]:要求划分后和划分前 最小的 数据的混乱度 下降 [1]:要求划分后每个集合样本数目的最小值,若小于,不执行此划分直接作为叶子节点 """ # 选择最佳的划分条件 feat, val = chooseBestSplit(dataSet, leafType, errType, ops) if feat == None: return val # 中止条件 #创建树结构 retTree = {} retTree['spInd'] = feat #划分的特征idx retTree['spVal'] = val #划分的边界值 lSet, rSet = binSplitDataSet(dataSet, feat, val) # 递归调用 retTree['left'] = createTree(lSet, leafType, errType, ops) retTree['right'] = createTree(rSet, leafType, errType, ops) return retTree
2、树的后剪枝算法
根据测试数据决定是否对当前子树进行塌陷处理
def isTree(obj):
"""判断是否为一棵树"""
return (type(obj)==dict)
def getMean(tree):
"""该函数对树进行塌陷处理(即返回树平均值)"""
if isTree(tree['right']): tree['right'] = getMean(tree['right'])
if isTree(tree['left']): tree['left'] = getMean(tree['left'])
return (tree['left']+tree['right'])/2.0
def prune(tree, testData):
"""剪枝函数"""
if np.shape(testData)[0] == 0:
#若果没有测试数据,将整棵树(子树)进行塌陷处理器,
#因为以下的划分都过拟合了,对于提高没有任何意义
return getMean(tree)
if (isTree(tree['right']) or isTree(tree['left'])):
# 如果有一个孩子是一棵树,尝试分割测试集
lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
#递归调用
if isTree(tree['left']):
tree['left'] = prune(tree['left'], lSet)
if isTree(tree['right']):
tree['right'] = prune(tree['right'], rSet)
# 如果两个孩子是叶子节点,尝试是否可以合并
if not isTree(tree['left']) and not isTree(tree['right']):
lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
# 没有合并的误差
errorNoMerge = np.sum(np.power(lSet[:,-1] - tree['left'],2)) +\
np.sum(np.power(rSet[:,-1] - tree['right'],2))
# 整棵树的均值
treeMean = (tree['left']+tree['right'])/2.0
# 合并后的均值
errorMerge = np.sum(np.power(testData[:,-1] - treeMean,2))
if errorMerge < errorNoMerge:
print ("merging")
return treeMean
else: return tree
else: return tree3、模型树
类似于回归树,不同点在于:
- 记录的不是一个平均值,而是一个权重向量
比较划分的优劣的量度变成线性回归的代价
def linearSolve(dataSet): """使用最小二乘法计算线性回归权重""" m,n = np.shape(dataSet) X = np.mat(np.ones((m,n))); Y = np.mat(np.ones((m,1)))#create a copy of data with 1 in 0th postion X[:,1:n] = dataSet[:,0:n-1]; Y = dataSet[:,-1]#and strip out Y xTx = X.T*X if np.linalg.det(xTx) == 0.0: raise NameError('This matrix is singular, cannot do inverse,\n\ try increasing the second value of ops') ws = xTx.I * (X.T * Y) return ws,X,Y def modelLeaf(dataSet): """叶子节点""" ws, X, y = linearSolve(dataSet) return ws def modelErr(dataSet): """计算线性模型的误差""" ws, X, y = linearSolve(dataSet) yHat = X * ws return np.sum(np.power(y-yHat, 2)) # 其他代码通用