机器学习实战（Peter Harrington）阅读笔记（二）

十、利用K-均值聚类算法对未标注数据分组

1、K-均值聚类算法

创建k个点作为起始质心（经常是随机选择）
当任意一个点的簇分配结果发生改变时
	对数据集中的每个数据点
		对每个质心
			计算质心与数据点之间的距离
		将数据点分配到距其最近的簇
	对每一个簇，计算簇中所有点的均值并将均值作为质心

实现

def distEclud(vecA, vecB):
	"""欧拉距离"""
	return np.sqrt(np.sum(np.power(vecA - vecB, 2))) #la.norm(vecA-vecB)


def randCent(dataSet, k):
	"""随机质心"""
	n = np.shape(dataSet)[1]
	centroids = np.mat(np.zeros((k,n))) # 创建质心矩阵
	for j in range(n):
	# 针对每个特征的取值范围随机初始化每个质心的这个特征的值
		minJ = min(dataSet[:,j])
		rangeJ = float(np.max(dataSet[:,j]) - minJ)
		centroids[:,j] = np.mat(minJ + rangeJ * np.random.rand(k,1))
	return centroids


def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
	"""k均值聚类算法"""
	m = np.shape(dataSet)[0]
	# 记录每个样本的所归属的质心idx，和该样本和所属质心距离
	clusterAssment = np.mat(np.zeros((m,2)))

	centroids = createCent(dataSet, k) #创建质心
	clusterChanged = True
	while clusterChanged:
		clusterChanged = False
		for i in range(m):
		#遍历每一个样本，寻找距离最近的质点
			minDist = np.inf; minIndex = -1
			for j in range(k):
				distJI = distMeas(centroids[j,:],dataSet[i,:])
				if distJI < minDist:
					minDist = distJI; minIndex = j
			#如果该样本所属的质点发生变化，则说明没有达到最优
			if clusterAssment[i,0] != minIndex:
				clusterChanged = True
			# 记录质点
			clusterAssment[i,:] = minIndex,minDist**2
		# 重新计算每个质心，根据距离
		for cent in range(k):
			# 获得所有属于该质点的样本
			ptsInClust = dataSet[clusterAssment.A[:,0]==cent]
			# 计算这些样本的中心
			centroids[cent,:] = np.mean(ptsInClust, axis=0)
	return centroids, clusterAssment

2、二分K-均值算法

SSE（Sum of Squared Error，误差平方和）

该算法首先将所有点作为一个簇，然后将该簇一分为二。之后选择其中一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。上述基于SSE的划分过程不断重复，直到得到用户指定的簇数目为止。

伪代码

将所有点看成一个簇
当簇数目小于k时
	对于每一个簇
		计算总误差
		在给定的簇上面进行K-均值聚类（k=2）
		计算将该簇一分为二之后的总误差
	选择使得误差最小的那个簇进行划分操作

实现

def biKmeans(dataSet, k, distMeas=distEclud):
	"""二分K均值算法"""
	m = np.shape(dataSet)[0]
	# 记录每个样本的所归属的质心idx，和该样本和所属质心距离
	clusterAssment = np.mat(np.zeros((m,2)))

	# 初始化唯一质心，将所有点归为一个簇
	# 获取每个特征均值
	centroid0 = np.mean(dataSet, axis=0).tolist()[0]
	centList =[centroid0] #创建一个质心列表
	for j in range(m): #计算每个点的误差
		clusterAssment[j,1] = distMeas(np.mat(centroid0), dataSet[j,:])**2

	while (len(centList) < k): #只有当质心数目达到k
		lowestSSE = np.inf #初始化误差平方和
		for i in range(len(centList)): #针对每一个质心
			#获得所有属于该质点的样本
			ptsInCurrCluster = dataSet[clusterAssment.A[:,0]==i]
			#将该簇一分为二
			centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
			#计算SSE
			sseSplit = np.sum(splitClustAss[:,1])
			#其他簇的SSE
			sseNotSplit = np.sum(clusterAssment[np.nonzero(clusterAssment[:,0].A!=i)[0],1])
			print ("sseSplit, and notSplit: ", sseSplit, sseNotSplit)
			if (sseSplit + sseNotSplit) < lowestSSE: #更新该次划分
				bestCentToSplit = i
				bestNewCents = centroidMat #新的质心
				bestClustAss = splitClustAss.copy() #新的划分
				lowestSSE = sseSplit + sseNotSplit
		#将1的簇的样本更改为len(centList)
		bestClustAss[np.nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList)
		#将0号簇的样本更改为划分的id
		bestClustAss[np.nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
		print ('the bestCentToSplit is: ',bestCentToSplit)
		print ('the len of bestClustAss is: ', len(bestClustAss))
		#更新已经划分质心
		centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids
		#添加新的质心
		centList.append(bestNewCents[1,:].tolist()[0])
		#更新被二分的簇所属样本的簇和误差
		clusterAssment[np.nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss
	return np.mat(centList), clusterAssment

十一、使用Apriori算法进行关联分析

1、关联分析

关联分析是一种在大规模数据集中寻找有趣关系的任务。这些关系可以有两种形式：频繁项集或者关联规则。

频繁项集（frequent item sets）：是经常出现在一块的物品的集合，例如{葡萄酒，尿布, 豆奶}
关联规则（association rules）：暗示两个集项之间可能存在很强的关系，例如{尿布} ➞ {葡萄酒}

衡量标准

支持度（support）：用于衡量频繁项集的频繁程度，计算公式样本中存在该集项数目 / 样本数
可信度或置信度（confidence）：用于衡量两个集项之间关系的强弱，{尿布} ➞ {葡萄酒}的计算公式为支持度({尿布, 葡萄酒})/支持度({尿布})

著名案例：

啤酒与尿布故事

2、Apriori原理及实现

通过去除小于给定支持度的集项及其超集，来缓解组合爆炸情况，以提高速度

原理：非常容易理解，当一个集项小于给定的支持度，那么其超集的支持度一定也小于给定的支持度

（1）辅助函数

import numpy as np

def loadDataSet():
	return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]

def createC1(dataSet):
	# 创建只有一个元素的集项
	C1 = []
	for transaction in dataSet:
		for item in transaction:
			if not [item] in C1:
				C1.append([item])

	C1.sort()
	return list(map(frozenset, C1))#use frozen set so we
							#can use it as a key in a dict

def scanD(D, Ck, minSupport):
	""" 它有三个参数，分别是
	数据集、
	候选项集列表Ck
	以及感兴趣项集的最小支持度minSupport
	返回
	"""
	# 一个项集的支持度（support）被定义为数据集中包含该项集的记录所占的比例。
	# 可信度或置信度（confidence）
	# 是针对一条诸如{尿布} ➞ {葡萄酒}的关联规则来定义的
	# “支持度({尿布, 葡萄酒})/支持度({尿布})”
	ssCnt = {}
	for tid in D:
		for can in Ck:
			if can.issubset(tid):
				if not can in ssCnt.keys(): ssCnt[can]=1
				else: ssCnt[can] += 1
	numItems = float(len(D))
	retList = []
	supportData = {}
	for key in ssCnt:
		support = ssCnt[key]/numItems
		if support >= minSupport:
			retList.insert(0,key) #在列表头添加这个集合
		supportData[key] = support #记录支持度
	return retList, supportData


def aprioriGen(Lk, k): #creates Ck
	"""创建Ck，也就是元素元素数为k的集项"""
	retList = []
	lenLk = len(Lk)
	for i in range(lenLk):
		for j in range(i+1, lenLk):
			# 提取每个元素的的前k-1个元素
			L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2]
			L1.sort(); L2.sort()
			if L1==L2: #如果前k-1个元素相等，才执行并集操作，避免重复
				retList.append(Lk[i] | Lk[j]) #并集
	return retList

实现算法

def apriori(dataSet, minSupport = 0.5):
	"""找到频繁项集，并计算支持度"""
	C1 = createC1(dataSet) #创建C1
	D = list(map(set, dataSet)) #将数据转换为集合
	L1, supportData = scanD(D, C1, minSupport) # 计算C1的支持度
	L = [L1]
	k = 2
	while (len(L[k-2]) > 0):
		Ck = aprioriGen(L[k-2], k)
		Lk, supK = scanD(D, Ck, minSupport)#scan DB to get Lk
		supportData.update(supK) #将新的支持度添加到列表上
		L.append(Lk) #将符合要求置信度的集项添加到列表中
		k += 1
	return L, supportData

3、从频繁项集中挖掘关联规则

def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
	m = len(H[0])
	if (len(freqSet) > (m + 1)): #try further merging
		Hmp1 = aprioriGen(H, m+1)#create Hm+1 new candidates
		Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
		if (len(Hmp1) > 1):	#need at least two sets to merge
			rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)

def calcConf(freqSet, H, supportData, brl, minConf=0.7):
	prunedH = [] #create new list to return
	for conseq in H:
		conf = supportData[freqSet]/supportData[freqSet-conseq] #calc confidence
		if conf >= minConf:
			print (freqSet-conseq,'-->',conseq,'conf:',conf)
			brl.append((freqSet-conseq, conseq, conf))
			prunedH.append(conseq)
	return prunedH

def generateRules(L, supportData, minConf=0.7):
	"""
	生成关联规则
	L和supportData 来自 scanD 函数
    minConf为最小支持度
    返回一个元组列表类型为样例：
    {尿布} ➞ {葡萄酒}
    [({尿布}, {葡萄酒}, 置信度)]
    """
	bigRuleList = []
	for i in range(1, len(L)): #只需要获取元素大于2的集合
		for freqSet in L[i]:
			H1 = [frozenset([item]) for item in freqSet] # 将集合拆分为单元素集合列表
			if (i > 1):
				rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
			else:
				calcConf(freqSet, H1, supportData, bigRuleList, minConf)
	return bigRuleList

十二、使用FP-growth算法来高效发现频繁项集

1、FP树：用于编码数据集的有效方式

对于这个数据集

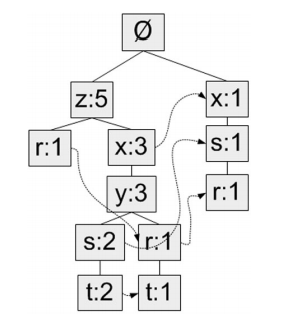示例数据要生成的fp树，最小数目为3 fp树在程序中要表现的结构 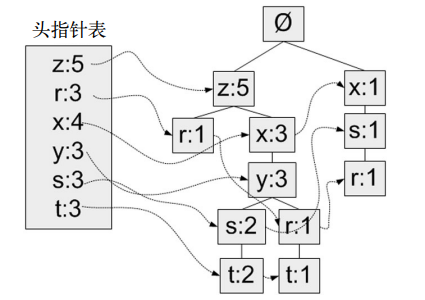fp树构建树的过程

第一次扫描样本，统计每个元素出现的次数
第二次扫描样本，针对每一个样本
- 按照出现频次从大到小排序
- 对于第i元素，判断这个元素是否在树的第i+1层出现过
  - 若出现过，该节点+1
  - 若没出现过，创建该节点，并设置各种指针

2、构建FP树

实现

def loadSimpDat():
    simpDat = [['r', 'z', 'h', 'j', 'p'],
               ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
               ['z'],
               ['r', 'x', 'n', 'o', 's'],
               ['y', 'r', 'x', 'z', 'q', 't', 'p'],
               ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
    return simpDat

def createInitSet(dataSet):
    """对数据进行预处理，为的是createTree函数可以复用"""
    retDict = {}
    for trans in dataSet:
        retDict[frozenset(trans)] = 1
    return retDict


class treeNode:
    """树的一个节点"""
    def __init__(self, nameValue, numOccur, parentNode):
        self.name = nameValue # 节点名
        self.count = numOccur # 数目
        self.nodeLink = None # 链接相似的元素项
        self.parent = parentNode      #needs to be updated
        self.children = {}

    def inc(self, numOccur):
        self.count += numOccur

    def disp(self, ind=1):
        print ('  '*ind, self.name, ' ', self.count)
        for child in self.children.values():
            child.disp(ind+1)

def updateHeader(nodeToTest, targetNode):
    #不使用递归实现，更新头指针
    while (nodeToTest.nodeLink != None):    #Do not use recursion to traverse a linked list!
        nodeToTest = nodeToTest.nodeLink
    nodeToTest.nodeLink = targetNode

def updateTree(items, inTree, headerTable, count):
    """更新树参数为：
    排序后的样本，树的头指针，头指针表，该样本出现的次数"""
    if items[0] in inTree.children: #检查当前元素是否在此次层
        inTree.children[items[0]].inc(count) #增加计数
    else:   #创建新的节点
        inTree.children[items[0]] = treeNode(items[0], count, inTree)
        #更新头表
        if headerTable[items[0]][1] == None:
            headerTable[items[0]][1] = inTree.children[items[0]]
        else:
            updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
    if len(items) > 1:#递归调用
        updateTree(items[1::], inTree.children[items[0]], headerTable, count)



def createTree(dataSet, minSup=1):
    """从数据集创建FP树  but do not mine"""
    headerTable = {} # 头指针
    # 遍历数据集两次
    for trans in dataSet: # 第一遍遍历统计出现的频率
        for item in trans:
            headerTable[item] = headerTable.get(item, 0) + dataSet[trans]

    delKey = []
    for k in headerTable.keys(): # 移除不满足最小支持度的元素
        if headerTable[k] < minSup:
            delKey.append(k)

    for k in delKey:
        del(headerTable[k])

    freqItemSet = set(headerTable.keys())
    if len(freqItemSet) == 0: return None, None  #如果没有元素则退出

    for k in headerTable:
        headerTable[k] = [headerTable[k], None] #reformat headerTable to use Node link

    #print(headerTable)
    retTree = treeNode('Null Set', 1, None) # 创建树的根节点
    for tranSet, count in dataSet.items():  # 第二遍遍历统计出现的频率
        localD = {}
        # 将此样本按照出现频率进行排序
        for item in tranSet:
            if item in freqItemSet:
                localD[item] = headerTable[item][0]
       # print(localD)
        if len(localD) > 0:
            orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)]
            #更新频繁树
            updateTree(orderedItems, retTree, headerTable, count)
    return retTree, headerTable #返回树和头表

测试算法

import fpGrowth

#测试数据
testData = fpGrowth.loadSimpDat()
intData = fpGrowth.createInitSet(testData)
#构建条件为{}的fp树
retTree, headerTable = fpGrowth.createTree(intData, 3)
retTree.disp()

3、从一棵FP树中挖掘频繁项集

实现步骤

从FP树中获得条件模式基
利用条件模式基，构建一个条件FP树（也就是上一步实现的函数）；
递归调用

（1）抽取条件基

首先从上一节发现的已经保存在头指针表中的单个频繁元素项开始。对于每一个元素项，获得其对应的条件模式基（conditional pattern base）。条件模式基是以所查找元素项为结尾的路径集合。每一条路径其实都是一条前缀路径（prefix path）。简而言之，一条前缀路径是介于所查找元素项与树根节点之间的所有内容。

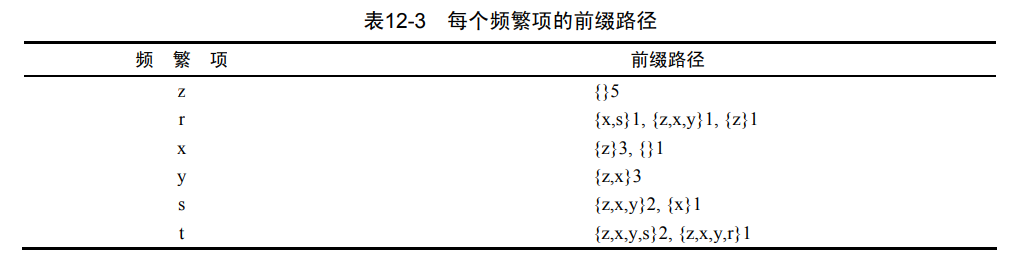
抽取条件模式基

实现

def ascendTree(leafNode, prefixPath):
    # 递归从叶子节点到根节点
    if leafNode.parent != None:
        prefixPath.append(leafNode.name)
        ascendTree(leafNode.parent, prefixPath)


def findPrefixPath(basePat, treeNode): #treeNode 来自头指针表
    """ 发现以给定元素项结尾的所有路径的函数 """
    condPats = {}
    while treeNode != None:
        prefixPath = []
        ascendTree(treeNode, prefixPath)
        if len(prefixPath) > 1:
            condPats[frozenset(prefixPath[1:])] = treeNode.count
        treeNode = treeNode.nodeLink
    return condPats

def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
    """一直递归创建条件fp树"""
    # 对头指针表，按照出现次数进行排序
    bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1][0])]
    for basePat in bigL:  #从最小的开始执行
        newFreqSet = preFix.copy() #记录一下上一个前缀（条件）
        newFreqSet.add(basePat)
        freqItemList.append(newFreqSet) #记录这个频繁集
        condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
        #2. construct cond FP-tree from cond. pattern base
        # 2. 构建条件fp树
        myCondTree, myHead = createTree(condPattBases, minSup)
        if myHead != None: #3. 头指针非空，递归操作
            mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)

测试

#输出发现的频繁集
freqItems = []
fpGrowth.mineTree(retTree, headerTable, 3, set([]), freqItems)
print(len(freqItems))
print(freqItems)

十三、利用PCA来简化数据

1、降维技术

目的：

使得数据集更易使用
降低很多算法的计算开销
去除噪声
使得结果易懂

方法

主成分分析（Principal Component Analysis，PCA）
因子分析（Factor Analysis）
独立成分分析（Independent Component Analysis，ICA）

2、PCA

算法伪代码

去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值从大到小排序
保留最上面的N个特征向量
将数据转换到上述N个特征向量构建的新空间中

编程实现

import numpy as np
import matplotlib
import matplotlib.pyplot as plt

def loadDataSet(fileName, delim='\t'):
	fr = open(fileName)
	stringArr = [line.strip().split(delim) for line in fr.readlines()]
	datArr = [list(map(float,line)) for line in stringArr]
	return np.mat(datArr)

def pca(dataMat, topNfeat=9999999):
	meanVals = np.mean(dataMat, axis=0)
	meanRemoved = dataMat - meanVals #remove mean
	covMat = np.cov(meanRemoved, rowvar=0)
	eigVals,eigVects = np.linalg.eig(np.mat(covMat))
	eigValInd = np.argsort(eigVals)			#sort, sort goes smallest to largest
	eigValInd = eigValInd[:-(topNfeat+1):-1]  #cut off unwanted dimensions
	redEigVects = eigVects[:,eigValInd]	   #reorganize eig vects largest to smallest
	lowDDataMat = meanRemoved * redEigVects#transform data into new dimensions
	reconMat = (lowDDataMat * redEigVects.T) + meanVals
	return lowDDataMat, reconMat

def draw(dataMat, reconMat):
	fig = plt.figure()
	ax = fig.add_subplot(111)
	ax.scatter(dataMat[:,0].flatten().A[0],
		dataMat[:, 1].flatten(), marker = '^', s=90)
	ax.scatter(reconMat[:,0].flatten().A[0],
		reconMat[:, 1].flatten(), marker = 'o', s=50, c='red')
	plt.show()

测试

import pca
import numpy as np

dataMat = pca.loadDataSet('testSet.txt')
lowDMat, reconMat = pca.pca(dataMat, 1)
print(np.shape(lowDMat))

pca.draw(dataMat, reconMat)

十四、利用SVD简化数据

参见推荐系统

十五、大数据与MapReduce

略