17 分钟
编译原理
目录
龙书:编译原理中文第二版
一、引论
该章节是对全书内容的概述,可能相对难以理解。很多内容细节在下文章节才有所解释。
1、编译器结构
(1)两个阶段
- 分析(对应编译器前端)
- 输入:源程序
- 输出:中间表示形式+符号表
- 综合(对应编译器的后端)
- 输入:中间表示+符号表
- 输出:目标程序
(2)主要步骤
- 词法分析
- 输入:源程序字符串流
- 输出:每个词素产生一个语法单元(一个元组
<token-name, attribute-value>)+符号表
- 语法分析
- 输入:语法单元序列+符号表
- 输出:语法树+符号表
- 语义分析
- 输入:语法树+符号表
- 职责:类型检查、自动类型转换
- 输出:语法树+符号表
- 中间代码生成
- 输入:语法树+符号表
- 输出:中间表示(三地址代码)+符号表
- 机器无关优化器(可选)
- 代码生成器
- 输入:中间表示(三地址代码)+符号表
- 输出:机器码序列
- 机器相关优化器
相关说明:
- 符号表贯穿始终
- 优化器可选,要保证正确前提下,提供较好的优化
- 前端部分为中间代码生成之前的部分
- 后端部分为中间代码生成之后的部分
二、一个简答的语法制导翻译器
该章节是利用编译原理实现的一个小功能的例子,用到了很多下文才使用知识。
2、语法定义
一个文法的例子(if else)
- 形式:
if(expr) stmt else stmt - 构造规则:
stmt → if(expr) stmt else stmt→读作:可以有如下形式,这种规则称为产生式- 关键字叫做:终结符号
- 变量叫做:非终结符号
(1)上下文无关文法定义
可以理解为C语言中的宏定义
四个元素:
- 一个终结符号集合(词法单元,类似于宏替换后的最终形式)
- 一个非终结符号集合(变量,可以被替换的对象)
- 一个产生式集合(替换规则)
- 指定一个非终结符号作为开始符号
例子1:10以内自然数+-法表达式
list -> list + digit
list -> list - digit
list -> digit
digit -> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9简化的写
list -> list + digit | list - digit | digit
digit -> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9- 文法开始符号为 list
- 终结符号为
+ - 0 1 2 3 4 5 6 7 8 9 - 非终结符号为
list digit - 空字符传定义为
ε
(2)推导
用途
用于语法分析:给出一个终结符号串作为输入,找出从文法的开始符号推到出这个串的方法(推导),如果做不到则报告语法错误
例子2:函数调用文法
call -> id ( optparams )
optparams -> params | ε
params -> params , param | param(3)语法分析树
定义
- 根节点为文法开始符号
- 每个叶子节点为终结符号或者
ε - 每个非叶子节点(内部节点)为非终结符号
A->XYZ绘制成树- A是根节点
- X是从左到右第一个树
- Y是从左到右第二个树
- Z是从左到右第三个树
注意: 语法分析树仅仅是上下文无关语法的语法一种具体的表现形式,用于在语法分析阶段产生抽象语法树,与抽象语法树是两个东西。
(4)二义性
当一个终结字符串存在两个及以上的语法分析树及为出现二义性
例子3:10以内自然数+-法表达式的二义性文法
string = string + string | string - string | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9主要问题在于没有体现结合性
(5)运算符的结合性
从左到右结合的写法(左结合)
left -> left op id | id从右到左结合的写法(右结合)
right -> id op right | id- id为标识符
- op为操作符
(6)运算符优先级
例子4四则运算的文法
expr -> expr + term | expr - term | term
term -> term * factor | term / factor | factor
factor -> digit | (expr)- expr 为表达式
- term 为单项式
- factor为因子
优先级和结合性的文法定义技巧:
- 将打的概念抽象为小的概念的结合,概念的划分按照优先级最低的符号划分,层层划分直到终结因子
- 比如
+-*/优先级最低为+-,所以:- 一个表达式由多个单项式
+-结合组成 - 一个单项式由多个因子
*/结合而成 - 一个因子为一个数字或者一个
(表达式)
- 一个表达式由多个单项式
- 比如
4、语法分析
使用 文法规则 检查目标串是否符合语法
方法:
- 自顶而下(受欢迎:因为效率高)
- 自低向上(效率低,通用性高)
(1)自底而下的方法
- 为标号A选择一个产生式,并为该产生式中的各个符号构造出N个子节点(如何选择需要讨论:就是一种试错过程)
- 寻找分析书的左边的未被扩展的非终结符号作为A再次执行上一步,递归下去
例子5:程序语句语句语法文法
stmt -> expr;
| if(expr) stmt
| for(optexpr; optexpr;optexpr) stmt
| other
optexpr -> ε
| expr输入
for(;expr;expr) other(2)预测分支法
递归下降分析法
当每个符号都能无二义性的选择一个产生式,此时的递归试探收敛为线性唯一确定的情况(因为每个产生式都以终结符号开头)
上面的例子就符合
此时就可以以 O(n)的复杂度构建语法树
(5)左递归
如果出现类似expr -> expr + term 的形式或混合形式,将陷入无线循环。左递归是可以消除的
5、简单的表达式翻译器
(1)抽象语法树
每个内部结代表一个运算符,该节点的子节点为运算分量
(2)消除左递归
A -> Aα|Aβ|γ 转化为等价形式
A -> γR
R -> αR | βR | ε例子6:10以内加减法文法
expr -> expr + term
| expr - term
| term
term -> 1|2|3|4|5|6|7|8|9|0消除左递归的文法
expr -> term rest
rest -> + term rest
| - term rest
| ε
term -> 1|2|3|4|5|6|7|8|9|0Java版的一个实现
package cn.rectcircle.dragonbook.ch02;
import java.io.IOException;
/**
* 十以内自然数+-法 原始文法
*
* <pre>
* expr -> expr + term
* | expr - term
* | term
* term -> 1|2|3|4|5|6|7|8|9|0
* </pre>
*
* 消除左递归后的文法
*
* <pre>
* expr -> term rest
* rest -> + term rest
* | - term rest
* | ε
* term -> 1|2|3|4|5|6|7|8|9|0
* </pre>
*/
class Parser {
static int lookahead;
public Parser() throws IOException {
lookahead = System.in.read();
}
/**
* 非终结符号expr
*/
void expr() throws IOException {
term();
rest();
}
/**
* rest
*/
void rest() throws IOException {
// 尾递归,可以优化为循环
if (lookahead=='+'){
match('+'); term(); System.out.print('+'); rest();
} else if(lookahead=='-'){
match('-'); term(); System.out.print('-'); rest();
} else if(lookahead=='\n' || lookahead == -1) { // 相当于空串 ε 流式处理的终结符
return;
} else {
throw new Error("syntax error");
}
}
/**
* 终结符号数字
*/
void term() throws IOException {
if(Character.isDigit((char) lookahead)){
System.out.write((char) lookahead); match(lookahead);
} else {
throw new Error("syntax error");
}
}
/**
* 移动游标
*/
void match(int t) throws IOException {
if (lookahead==t) lookahead = System.in.read();
else throw new Error("syntax error");
}
}
/**
* 解析10以内自然数加减法是否存在语法错误,并转换为后缀表达式并输出
*/
public class Postfix {
public static void main(String[] args) throws IOException {
Parser parser = new Parser();
parser.expr();
System.out.println();
}
}6、词法分析
例子7:自然数四则运算文法
expr -> expr + term
| expr - term
| term
term -> term * factor
| term / factor
| factor
factor -> (expr)
| num
| id词法分析器需要处理的事情
- 一般的词法分析器都会去除空白和注释
- 预读:分析存在元素大于一个字符时
- 常量(字面量):需要将常量比如说数字转换为一个词法单元(元组)
<num, 12> - 识别关键字和标识符:关键字类似
for、if,标识符值变量名等,通常看作终结符号,比如<id, "count">、<id, "for">
下面实现例子7中的词法分析器
package cn.rectcircle.dragonbook.ch02.lexer;
/**
* Token词法单元父类
*/
public class Token {
public final int tag;
public Token(int tag) {
this.tag = tag;
}
}package cn.rectcircle.dragonbook.ch02.lexer;
/**
* 标签枚举
*/
public class Tag {
public final static int NUM = 256;
public final static int ID = 257;
public final static int TRUE = 258;
public final static int FALSE = 259;
}package cn.rectcircle.dragonbook.ch02.lexer;
/**
* 数字词素
*/
public class Num extends Token{
public final int value;
public Num(int value) {
super(Tag.NUM);
this.value = value;
}
}package cn.rectcircle.dragonbook.ch02.lexer;
/**
* 关键字or保留字词素
*/
public class Word extends Token {
public final String lexeme;
public Word(int tag, String lexeme) {
super(tag);
this.lexeme = lexeme;
}
}package cn.rectcircle.dragonbook.ch02.lexer;
import java.io.IOException;
import java.util.HashMap;
import java.util.Map;
/**
* 四则运算词法分析器,实现的文法如下
*
* <pre>
expr -> expr + term
| expr - term
| term
term -> term * factor
| term / factor
| factor
factor -> (expr)
| num
| id
* </pre>
*/
public class Lexer {
public int line = 1;
private char peek = ' ';
/**
* 关键字/保留字/标识符保持单例
*/
private Map<String, Word> words = new HashMap<>();
public Lexer() {
reserve(new Word(Tag.TRUE, "true"));
reserve(new Word(Tag.FALSE, "false"));
}
/**
* 将关键字词/标识符素放入
*/
private void reserve(Word t) {
words.put(t.lexeme, t);
}
public Token scan() throws IOException {
// 处理多余空白字符
for (;; peek = (char) System.in.read()) {
if (peek == ' ' || peek == '\t') {
continue;
} else if (peek == '\n') {
line++;
} else {
break;
}
}
// 下面根据第一个有效字符的情况进行预读
// 第一个字符是数字:解析成int
if (Character.isDigit(peek)) {
int v = 0;
do {
v = 10 * v + Character.digit(peek, 10);
peek = (char) System.in.read();
} while (Character.isDigit(peek));
return new Num(v);
}
// 第一个字符是字母
if (Character.isLetter(peek)) {
StringBuilder sb = new StringBuilder();
do {
sb.append(peek);
peek = (char) System.in.read();
} while (Character.isLetterOrDigit(peek));
String s = sb.toString();
Word w = words.get(s);
if (w != null) {
return w;
}
w = new Word(Tag.ID, s);
reserve(w);
return w;
}
Token t = new Token(peek);
peek = ' ';
return t;
}
}7、符号表
用于存放各种标识符信息的表,一段程序存在多张符号表,这些符号表组成一棵树型结构。在某一时刻表现为一个链表。每个符号表代表一个作用域。符号表中的条目主要包含标识符名和类型信息两个部分。
package cn.rectcircle.dragonbook.ch02.symbols;
/**
* 符号
*/
public class Symbol {
}package cn.rectcircle.dragonbook.ch02.symbols;
import java.util.HashMap;
import java.util.Map;
/**
* 符号表(作用域),是一个树形结构。 每个符号表为一个节点,其存在一个指向父节点(上层作用域)的指针
*/
public class Env {
private Map<String, Symbol> table;
protected Env prev;
public Env(Env prev) {
this.table = new HashMap<>();
this.prev = prev;
}
public void put(String s, Symbol sym) {
table.put(s, sym);
}
public Symbol get(String s) {
for (Env e = this; e != null; e = e.prev) {
Symbol sym = e.table.get(s);
if (sym != null) {
return sym;
}
}
return null;
}
}构造过程
- 初始化一个top作用域符号表,作为
current - 每当遇到一个
{则创建一个新的作用域,其prev为当前current,并赋值给current - 每当遇到一个
}则current=current.prev
8、生成中间代码
(1)中间代码的两种表达形式
- 树形结构(抽象语法树)
- 线性表达方式(三地址代码)
- 方便进行优化
编译器一般两者同时生成,但是不会保存语法树的全部部分,当不需要的时候就会进行释放
(2)语法树的构造
例子8:一个表达式和语句块的文法
program -> block
block -> '{' stmts '}'
stmts -> stmts stmt
| ε
stmt -> expr;
| if (expr) stmt
| while (expr) stmt
| do stmt while(expr);
| block
expr -> rel = expr
| rel
rel -> rel < add
| rel <= add
| add
add -> add + term
| term
term -> term * factor
| factor
factor -> (expr)
| numstmt为一个语句expr为一个表达式
可以将上述的文法在程序中实现为一个抽象语法树
在实现过程中:
- Node是所有类的祖宗类,包含一个属性
n- Stmt是Node的子类,代表语句块
- Seq是Stmt的子类
- If等是Stmt的子类
- Eval是Stmt子类
- Expr是Node的子类,代表表达式
- Assign = 赋值
- Cond && 条件
- Rel < 比较
- Op +、- 二元运算
- Not ! 非
- Minus - 负
- Access [] 访问
- Stmt是Node的子类,代表语句块
(3)静态检查
- 语法检查
- 类型检查
(4)三地址码
通过遍历语法树可以生成三地址码,以进行分析综合
三地址码指形如下的指令片段
x = y op z数组形如下
x[y] = z
x = y[z]流程控制:
ifFalse x goto L
ifTrue x goto L
goto L拷贝
x = y对表达式的翻译会产生临时的名字
9、第二章总结
- 构造一个语法直到翻译器要从源语言的文法开始。文法定义见上
- 表述一个翻译器附加属性很重要,比如变量的名字,字面量的值
- 词法分析逐一输入字符构建出词法单元(一个元组比如
<id, 'name'>)流,翻译器使用符号表存放保留字和已经遇到的标识符 - 语法分析要解决的是从一个文法开始符号推导出终结符号串,概念上会创建一个
语法分析树,根节点为文法开始符号,每个非叶子节点代表一个产生式,语法分析树的叶子节点从左到右组成终结符号串 - 预测分支法,采用自定而下方法可以建立高效的语法分析器。
- 语法制导翻译,通过在文法中添加规则或程序片段完成
- 语法分析结果是源代码一种中间结果,称为中间代码,有两种表现形式
抽象语法树和三地址代码 - 符号表用于存放标识符信息,声明时放入符号表,遇到时再使用
另
三、词法分析
1、词法分析器的作用
读入源程序,将其转换为词素,转换为词法单元,输出词法单元序列,每个词法单元对应一个词素。当发现一个标识符词素时,这个词素添加到符号表中。
- 读取源程序
- 识别次数
- 过滤注释和空白
- 生成错误消息与源程序位置关联
词法分析器分为两个阶段
- 扫描阶段:删除注释和压缩空白字符
- 词法分析阶段:生成词法单元
分成词法分析和语法分析的原因
- 简化设计,专注于一个任务,有助于设计语法
- 提高编译器的效率
- 增强编译器可移植性
术语
- 词法单元:由一个词法单元名和一个可选属性组成
- 名称表示某种词法单元的抽象符号,比如关键字、字符序列
- 模式:描述一个词法单元的词素可能具有的形式(识别一个字符序列是某词法单元的定义)
- 词素:源程序的一个字符序列,和某个词法单元匹配,并被词法分析器识别为该词法单元的一个实例
| 词法单元 | 非正式描述 | 词素实例 |
|---|---|---|
| if | 字符i,f | if |
| else | 字符e,l,s,e | else |
| comparison | >, < 等 | <=,!= |
| id | 字母开头的串 | pi |
| number | 任何数字常量 | 3.124,1 |
| literal | 两个”“之间除了”“之外的任意字符 | “string” |
大多数程序设计语言的词法单元
- 每个关键自由一个词法单元,其模式是其本身
- 表示运算符的词法单元,其模式是其本身
- 一个表示所有标识符的词法单元
- 一个或多个常量的词法单元,如数字或者字面量字符串
- 每一个标点符号有一个词法单元,比如左右括号,逗号,分号
词法单元的属性
- 比如标识符词法单元应该有一个属性,该属性是指向符号表的一个指针
词法错误:源程序中出现一个序列,没有可用的模式与之匹配
2、输入缓冲
- 每个缓冲区的大小一般是一个磁盘块的大小
- 一般采用多缓冲
- 程序维护了两个指针
- lexemeBegin:指向当前词素的开头位置
- forword指针:一直向前扫描,直到发现一个模式为止,如果forword处理到缓冲区尾部,将文件读取接下来的文件到下一个缓冲区内,一旦与某个模式匹配,则进行词素处理。然后将lexemeBegin指向forword的下一个位置。
3、词法单元规约
https://zhuanlan.zhihu.com/p/57915716 https://en.wikipedia.org/wiki/Regular_language https://en.wikipedia.org/wiki/Regular_expression http://aandds.com/attachments/regex/regex.pdf https://en.wikipedia.org/wiki/Stephen_Cole_Kleene
串和语言
- 字母表(Alphabet)是一个有限的符号集合,比如ascii码、Unicode码
- 串(String)是字母表中符号的一个有穷序列(其他的表述为:句子、字)
- 串
s的长度一般表示为|s| - 空串一般用
ε表示 - 前缀(prefix)
- 后缀(suffix)
- 子串(substring)
- 真前缀、真后缀、真子串:排除空串的集合
- 子序列(subsequence):从串中取出任意0个或者多个符号
- 串
- 串的运算:假设有 x = dog 、 y = house
- 连接,记做
xy,则xy = doghouseε是连接运算的单位元,任意串s,有sε = εs = s
- 乘积,记做
s^ii为阶数s^0 = εs^i = s^(i-1) s
- 连接,记做
- 语言(language)是给定字母表上任意一个有穷串的集合
- 语言的例子
∅{ε}- 所有语法正确的C程序的集合
- 语言的例子
语言的运算
- 并运算
L∪M = {s | s ∈ L 或 s ∈ M} - 连接运算
LM = { st | s ∈ L 且 t ∈ M} - Kleene闭包(closure)
L^* = L 连接0次或者多次得到集合L^0 = {ε}
- 正闭包(closure)
L^+ = L 连接1次或者多次得到集合
例子: L = {大小写字母} 单字符串组成的语言 D = {数字} 单字符串组成的语言
L∪D这个语言包含62个长度为1的串LD包含520长度为2的串的集合且首字母为字母L^4四个字母构成的串集合L^*所有字母构成的串的集合,包括空串L(L∪U)^*所有以字母开头,由数字和字母开头构成的串的集合D^+由一个或多个数位构成的串的集合
正则表达式
假设每个正则表达式 r 表示一个语言 L(r)(本质上正则表达式就是语言的运算的表达式;即每个正则表达式对应一个语言,对应的这门语言叫做正则集合),正则表达式的归纳定义如下
- 归纳基础
ε是正则表达式,则L(ε) = { ε },即该语言只包含一个空串- 如果
a是 某字母表的一个符号,则L(a) = { a }
- 归纳步骤
(r)|(s)是一个正则表达式,表示语言L(r)∪L(s)(r)(s)是一个正则表达式,表示语言L(r)L(s)(r)^*是一个正则表达式,表示语言(L(r))^*(r)是一个这则表达式,表示语言L(r),加括号不会影响表示的语言,只是表示优先级
为了去除括号和简化表示,需要定义如下规则
- 一元运算符具有最高优先级,且左结合
- 连接操作具有次高优先级,也是左结合
|拥有最低优先级,也是左结合
简化后的表示方式:
(a) | ((b)*c)等价于ab*c
正则表达式的代数定律
r|s = s|r表示|满足交换律r|(s|t) = (r|s)|t表示|满足结合律r(st) = (rs)t表示 连接 满足结合律r(s|t) = rs|rt; (s|t)r = sr|tr表示|满足分配率εr = rε =r表示ε是单位元r* = (r|ε)*表示闭包(*) 一定包含εr** = r*表示闭包(*)满足幂等性
例子 C 语言标识符 id 的 上下文无关文法(正则定义)
letter_ -> A|B|C|...|Z|a|b|...|z|_
digit -> 0|1|2|...|9
id -> letter_(letter_|digit)*正则表达式的扩展
*inx 类系统自带一个软件Lex最早使用的是一种正则表达式的扩展,本质上扩展的正则表达式都可以转化为经典正则表达式
- 一个或多个实例,使用后缀
+号。表示正闭包,和*具有相同的优先级和结合性。存在如下两个代数定律r* = r+|εr+ = rr* = r*r
- 零个或一个实例,使用后缀
?号。和*具有相同的优先级和结合性。r? = r|ε
- 字符类,一个正则表达式
a1|a2|...|an缩写为[a1a2...an],当序列在编码表中是连续的话可以简写为[a1-an]
Lex 全部语法如下
| 表达式 | 匹配 | 例子 |
|---|---|---|
| c | 单个非运算字符c | a |
| \c | 字符c的字面值(转义) | \* |
| “s” | 串s的字面值(转义) | “**” |
| . | 除换行符外任意字符 | a.*b |
| ^ | 一行的开始 | ^abc |
$ | 一行的结尾 | abc$ |
[s] | 字符串s中的任意字符 | [abc] |
| r* | 0个或多个 | a* |
| r+ | 1个或多个 | a+ |
| r? | 0个或1个 | a? |
| r{m,n} | 最少m个最多n个 | a{1,5} |
| r1r2 | r1连接r2 | ab |
| `r1 | r2` | r1并r2 |
| ® | 和r相通 | (a) |
| r1/r2 | 后面跟有r2时的r1 | abc/123 |
这样以上的例子可以简化为
letter_ -> [A-Za-z_]
digit -> [0-9]
id -> letter_(letter_|digit)*4、词法单元的识别
- 状态转换图
KMP算法:
- 计算trie失效函数:f(s)
- s为失效的地方(从1开始)
- f(s)的含义:满足
b[0:len] == b[s-len:s],f(s) = max(len)
- 使用模式串进行匹配,如果失效后,模式串向右移动
s-f(s)字符
b="ababaa"的失效函数
| s | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| f(s) | 0 | 0 | 1 | 2 | 3 | 1 |
| b[s-1] | a | b | a | b | a | a |
构造过程
b = "ababaa";
t = 0; // 前缀的长度(下一个字符的下标)
f[1] = 0;
for(int s=1; s<n; s++){ // 此s表示b的下标(从0开始)
while(t>0 && b[s] != b[t]) t = f[t]; //找到一个最长前缀==后缀,直到长度为0。
if(b[s] == b[t]){ t=t+1; f[s+1] = t;} // 如果t==0 此句不执行
else f[s+1] = 0;
}匹配过程
a = "fabababaa";
s = 0;
for(int i=0; 0<m; i++){
while(s>0 && a[i] != b[s]) s = f[s]; //发生失配,一直进行回退,直到s==0
if(a[i] == b[s]) s = s + 1; // 如果回退到了s==0,此不执行,直接跳到i++
if(s == n) return i;
}
return -1;KMP算法扩展:使用多模式串,例如下待匹配的模式串
heshehishers
按照输入序构造一个字典树,如下图所示
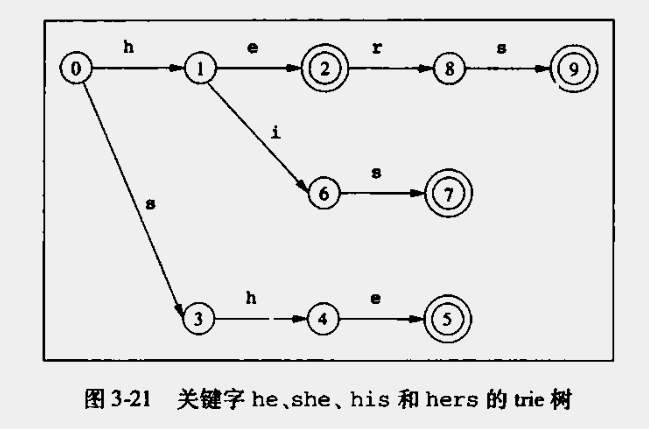
- 给每个节点编号,用于失效函数
- 两个圆圈表示终结点,当匹配到该字符则直接返回(如果在中间需要考虑是否贪婪)
构造的失效函数如下:
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| f(s) | 0 | 0 | 0 | 1 | 2 | 0 | 3 | 0 | 3 |
6、有穷自动机
本质上是一个状态转换图:
- 对输入只能简单回答是或否
- 分为两类
- 不确定有穷自动机(NFA):一个符号可以标记离开该状态的多条边
- 确定的有穷自动机(DFA):一个符号只能标记离开该状态的一条边
(1)不确定的有穷自动机
组成
- 一个有穷的状态集合
S - 一个输入符号集合
∑,即输入字母表,假设空串ε不是∑的元素 - 一个状态转换函数,它为
∑∪{ε}中每个符号都给出了相应的后记状态的集合 - S中的一个状态
s0指定为开始状态 - S的一个子集F被指定为
终止状态
例子
正则表达式(a|b)*abb的状态转换图
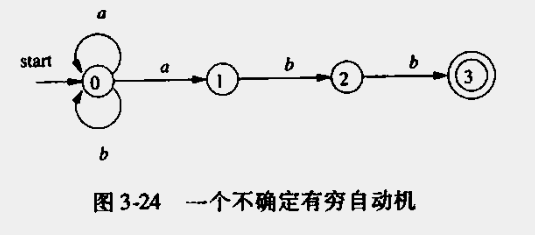
对应的状态转换表
| 状态 | a | b | ε |
|---|---|---|---|
| 0 | {0,1} | {0} | ∅ |
| 1 | ∅ | {2} | ∅ |
| 2 | ∅ | {3} | ∅ |
| 3 | ∅ | ∅ | ∅ |
可以看出编程实现的话会出现死循环
(2)确定的有穷自动机
确定有穷自动机是不确定有穷自动机的一个特例,在NFA基础上添加如下约束
- 没有ε之上的转换动作
- 每个状态s和输入符号a,只有一条边离开s
由于存在如上约束,编程实现十分容易,每个DFA都具有单一的模式识别能力
可以确定的是每个正则表达式都可以都可以转换成一个DFA。
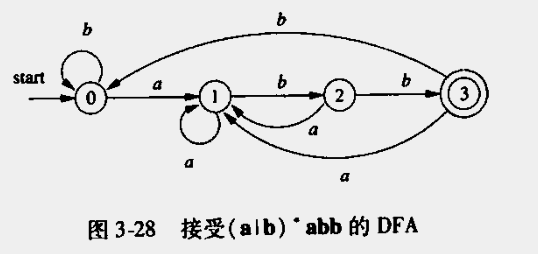
7、从正则表达式到自动机
正则表达式的实现方法
- 使用DFA进行匹配
- 使用NFA进行匹配
(1)从NFA到DFA的转换
子集构造法
- 输入:NFA N
- 输出:DFA D
相关概念:
N:表示NFA图D:表示DFA图Dstates:D的状态集合,每个元素是T,和是否被标记Dtran转换表:是D的表现形式。每一行是包含如下信息D的当前状态T和经过输入符号,到达的状态U的映射,记做Dtran[T,a]D的当前状态和N的状态集合的对应关系
s:表示N的一个状态s0:表示开始状态T,U,A,B,C:表示N某些状态的集合,同时表示D的一个状态F: 终止状态集合a:表示边标号输入符号集合中的一个元素0,1,2,3:表示N的状态编号- 核心函数
ε-closure(s):表示从状态s出发,只经过ε边可以到达的所有节点ε-closure(T):表示从T中的任意状态s出发,只经过ε边可以到达的所有状态的集合move(T,a):表示从T中的任意状态s出发,只经过a可以到达的所有状态的集合- 本质上是一个函数:
ε-closure(s) = ε-closure({s}) = move({s}, ε):实现上就是图的遍历
算法过程:
Dstates = {ε-closure(s0)} // 不添加标记
while(Dstates中存在未标记的元素){
T = Dstates中未标记的元素
for(针对每个输入符号){
U = ε-closure(move(T,a))
if(U not in Dstates)
将U添加到Dstates中并不添加标记
DTran[T, a] =U
}
}例子:正则表达式(a|b)*abb
NFA表示1
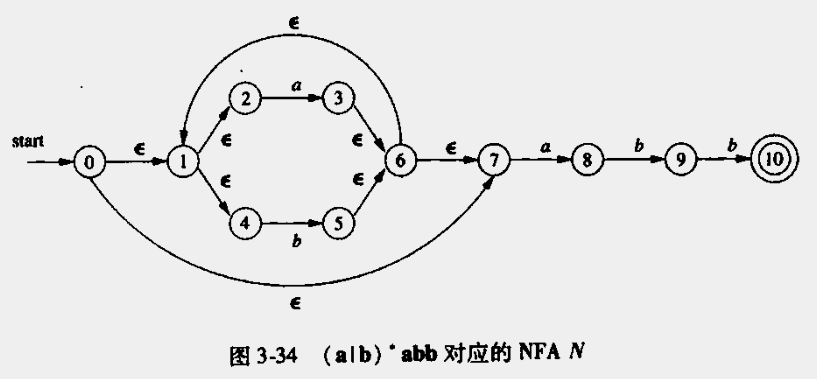
- 步骤1:
A = ε-closure(0) = {0, 1, 2, 4, 7}(一定包括0,0为起点可以通过ε到达自身),将A添加到Dstates - 步骤2:
- 从Dstates中取出A,将A进行标记
Dtran[A, a] = ε-closure(move(A, a)) = ε-closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = B(因为不在Dstates中),并添加到DstatesDtran[A, b] = ε-closure(move(A, b)) = ε-closure({5}) = {1, 2, 4, 6, 7} = C(因为不在Dstates中),并添加到Dstates
- 步骤…
最终得到:
| NFA状态 | DFA状态 | a | b |
|---|---|---|---|
| {0, 1, 2, 4, 7} | A | B | C |
| {1, 2, 3, 4, 6, 7, 8} | B | B | D |
| {1, 2, 4, 6, 7} | C | B | C |
| {1, 2, 4, 5, 6, 7, 9} | D | B | E |
| {1, 2, 4, 5, 6, 7, 10} | E | B | C |
NFA表示2

计算后得到的Dtran如下:
| NFA状态 | DFA状态 | a | b |
|---|---|---|---|
| {0} | A | B | A |
| {0, 1} | B | B | C |
| {0, 2} | C | B | D |
| {0, 3} | D | B | A |
(2)NFA的模拟
使用类似上文中的子集构造法直接匹配
S = ε-closure(s0)
c = nextC()
while(c != eof){
S = c-closure(move(S,c))]
c = nextChar()
}
if( |S∩F| != 0) return true
else return false(3)NFA的效率
O(k(m+n))
- k :带匹配字符串的长度
- n:状态数
- m:边数