参考: 文章1 https://github.com/txyyss/Lambda-Calculus 文章2 文章3

一、简单介绍

1、基本形式

丘奇等数学家给出了解决方法：λ演算。基本定义形式如下，

λ<变量>.<表达式>

2、简单示例

对于传统函数表示： $$ y = x^2 - 2x + 1 $$

使用lambda演算表示为： $$ \lambda x.x^2 - 2x + 1 $$

使用\(\beta\)规约（类似于函数调用求值），表示为： $$ (\lambda x.x^2 - 2x + 1) = 1-2*1+1=0 $$

多参数函数的lambda演算表示为： $$ λx.λy.2x+y $$

使用\(\beta\)规约（类似于函数调用求值），表示为： $$ (( λx.λy.2x+y) 1) 2 = ( λy.2+y) 2 = 4 $$

二、数学理论

1、形式化定义

定义 1 (λ 项) 假设我们有一个无穷的字符串集合,里面的元素被称为变量 (和程序语言中变量概念不同,这里就是指字符串本身)。那么 λ 项定义如下:

  1. 所有的变量都是 λ 项(名为原子);
  2. 若 M 和 N 是 λ 项,那么 (M N) 也是 λ 项(名为应用);
  3. 若 M 是 λ 项而 φ 是一个变量,那么 (λφ.M) 也是 λ 项(名为抽象)。

一些λ 项的例子

(λx.(x y))
(x(λx.(λx.x)))
((((a b) c) d) e)
(((λx.(λy.(y x))) a) b)
((λy.y) (λx.(x y))) (λx.(y z))

理解：

  • λ 项是一种形式语言,换句话说,就是一类特殊形式的字符串罢了,没有任何内在的意义,只是个“形式”。
  • 可以对照函数的形式理解lambda项, 那么变量是函数, 函数是一种抽象

2、替换

定义 2 (语法全等) 我们用恒等号 “≡” 表示两个 λ 项完全相同。换句话说 M≡N

表示 M 和 N 有完全相同的结构,且对应位置上的变量也完全相同。这意味着若 M N ≡ P Q 则 M ≡ P 且 N ≡ Q,若 λφ.M ≡ λψ.P 则 φ ≡ ψ 且 M ≡ P。

定义 3 (自由变量) 对一个 λ 项 P,我们可以定义 P 中自由变量的集合 FV(P) 如下:

  1. FV(φ) = {φ}
  2. FV(λφ.M) = FV(M) \ {φ}
  3. FV(M N) = FV(M) ∪ FV(N)

自由变量的例子

λ 项 P                   自由变量集合 FV(P)
λx.λy.x y a b            {a, b}
abcd                     {a, b, c, d}
x y λy.λx.x              {x, y}

理解：类似于非函数参数的变量，就是除去λ变量.变量后的集合

定义 4.(出现) 对于 λ 项 P 和 Q,可以定义一个二元关系出现。我们说 P 出现在 Q 中,是这样定义的:

  1. P 出现在 P 中;
  2. 若 P 出现在 M 中或 N 中,则 P 出现在 (M N) 中;
  3. 若 P 出现在 M 中或 P ≡ φ,则 P 出现在 (λφ.M) 中。

定义 5.(替换) 对任意 M, N, φ,定义 [N/φ] M 是把 M 中出现的自由变量 φ 替换成 N 后得到的结果,这个替换有可能改变部分约束变量名称以避免冲突。具体精确定义是一个对 M 的归纳定义:

  1. [N/φ] φ ≡ N 对所有满足 α ≢ φ 的原子 α
  2. [N/φ] α ≡ α
  3. N/φ ≡ ([N/φ] P [N/φ] Q)
  4. N/φ ≡ λφ.P 若 φ ∉ FV(P)
  5. N/φ ≡ λψ.P
  6. N/φ ≡ λψ.[N/φ] P 若 φ ∈ FV(P) 且 ψ ∉ FV(N)
  7. N/φ ≡ λη.[N/φ][η/ψ] P 若 φ ∈ FV(P) 且 ψ ∈ FV(N)

理解：就是执行简单替换，可以理解为函数参数替换为实参的过程

定义 6.(α 变换和 α 等价) 设 λφ.M 出现在一个 λ 项 P 中,且设 ψ ∉ FV(M),那么把 λφ.M 替换成 $$ λψ.[ψ/φ] M $$ 的操作被称为 P 的 α 变换。当且仅当若 P 经过有限步(包括零步) α 变换后,得到新的 λ 项 Q,则我们可以称 P 与 Q 是 α 等价的,又写作 $$ P ≡_\alpha Q $$

例子

λx.λy.x(x y) ≡ α λx.λv.x(x v) ≡ α λu.λv.u(u v)

可以理解为：函数参数的重命名后（同时替换函数中使用参数的地方），函数的功能不变

3、规约

β 规约可以这么直观的理解:我们可以把 (λφ.M) 看成是参数为 φ,函数体为 M 的一个函数;把 (M N) 看成是函数 M 作用到实际参数 N 上 4 。平时我们要是定义了函数 f(x) = x + 5,那么函数应用 f(6) 就是把 x + 5 中的 x 替换成 6,得到 f(6) = 6 + 5 = 11。

定义 7.(β 规约)形如 $$ (λφ.M) N $$ 的 λ 项被称为 β 可约式,对应的项 $$ [N/φ] M $$ 则称为 β 缩减项。当 P 中含有 (λφ.M) N 时,我们可以把 P 中的 (λφ.M) N 整体替换成 [N/φ] M,用 R 指称替换后的得到的项,那么我们说 P 被 β 缩减为 R,写做: $$ P ▷_{1β} R $$ 当 P 经过有限步(包括零步)的 β 缩减后得到 Q,则称 P 被 β 规约到 Q,写做: $$ P ▷_β Q $$

可以理解为调用函数：实质上式一种替换

替换

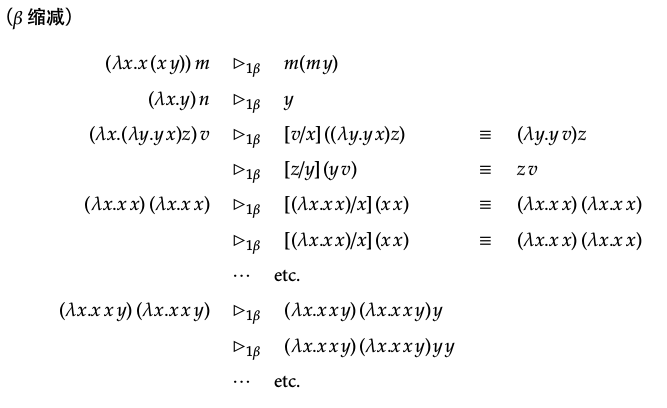
定义 8.(β 范式) 若一个 λ 项 Q 不含有 β 可约式,则称 Q 为 β 范式。若有 P 可被 β 规约到 Q,则称 Q 是 P 的 β 范式。

三、使用上面的定义定义程序语言

简单的例子其中\表示λ

Lambda> I = \x.x
Lambda> I a
a
Lambda> SWAP = \x.\y.y x
Lambda> SWAP a b
b a
Lambda> S = \x.\y.\z.x z(y z)
Lambda> S a b c
a c (b c)
Lambda> l = S I
Lambda> l m n
n (m n)

其他略

四、Y Combinator

1、使用BNF定义对lambda表达式

<expr> ::= <identifier>
<expr> ::= λ <identifier-list>. <expr>
<expr> ::= (<expr> <expr>)

2、使用lambda表达式实现递归

（1）以阶乘递归函数为例

伪代码

f(n):
	if n == 0  return 1
	else return n*f(n-1)

（2）lambda表达式的理想写法

let f = λ n. ( ifelse(n==0 1 n*f(n-1)) )
f(4)
  • let 表示给λ起别名
  • ifelse 为内置的λ表达式

问题：let f只是起到一个语法糖的作用，在它所代表的lambda表达式还没有完全定义出来之前你是不可以使用f这个名字的。

（3）另一次尝试：伪递归

let g = λ self. (λ n. ( ifelse(n==0 1 n*self(n-1))))
g(g 4)

问题：对g(g 4)进行β 规约，可以发现出现参数失配的问题

（4）成功的写法

let fac = λ self. (λ n. ( ifelse(n==0 1 n*self(self, n-1))))
fac(fac 4)

（5）简化函数声明——引入Y Combinator

虽然在（4）中已经实现了递归，但是不够简洁，这背离了函数式编程的原则。

简化目标：

存在一个 λ 表达式 Y，满足 f = Y(g)，其中：

  • f表示理想的递归表达式参见(2)中的f
  • g表示伪递归表达式参见(3)中的g

这样我们可以这么实现

let g = λ self. (λ n. ( ifelse(n==0 1 n*self(n-1))))
f = Y(g)
f(4)

这样导出的递归函数的签名才简洁有力

（6）不动点原理

符号约定：

  • f 表示理想的递归函数 let f = λ n. ( ifelse(n==0 1 n*f(n-1)) )
  • g 表示伪递归函数 g = λ self. (λ n. ( ifelse(n==0 1 n*self(n-1))))

假设 f 存在，则有

g(f)
= λ self. (λ n. ( ifelse(n==0 1 n*self(n-1)))) (f)
= λ n. ( ifelse(n==0 1 n*f(n-1)))
= f

可以得到：g(f) = f

这就是不动点原理，对于g来说，f就是这个不动点

一般化的描述就是，对任一伪递归F（伪递归F是给理想递归f加一个self参数从而得到的），必存在一个理想f，满足F(f) = f。

有了不动点原理g(f) = f 便可以轻易的推导出 Y的表达式：

Y(g) = f = g(f) = g(Y(g))

因此

Y(g) = g(Y(g))

（7）构造出Y

表达式Y(g) = g(Y(g))又是一个递归函数，类似于上面不优雅的实现：

let Y_gen = λ self. (λ g. (g(self(self g))) )
let Y = λ g. Y_gen(Y_gen)

写成嵌套表达式

let Y = λ g.(
			let Y_gen = λ self. (g(self(self)))
			Y_gen(Y_gen)
		)

3、scala模拟实现Y Combinator

参考： 1 2

	//Y Combinator实现
	def Y[T](g: (T => T) => (T => T)): (T => T) = g(Y(g))(_)
	//阶乘算法伪递归
	def g(self: Int => Int)(n:Int):Int = if(n==1) 1 else n*self(n-1)
	//生成完美递归函数
	val fac = Y(g)
	println(fac(3)) //测试