9 分钟
Tom Mitchell机器学习课程
http://www.cs.cmu.edu/~ninamf/courses/601sp15/lectures.shtml 搜索 汤姆·米切尔(Tom Mitchell)《机器学习》
一、绪论
1、学习问题的标准描述
(1)机器学习定义
对于某类任务 T 和性能度量 P,如果一个计算机程序在 T 上以 P 衡量的性能随着经验 E 而自我完善,那么我们称这个计算机程序在从经验 E 学习
例如:西洋跳棋学习问题
- 任务 T:下西洋跳棋
- 性能标准 P:比赛中击败对手的百分比
- 训练经验 E:和自己进行对弈
2、设计一个学习系统
(1)选择目标函数
ChooseMove:B→M :表示这个函数以合法棋局集合中的棋盘状态作为输入,并从合法走子集合中产生某个走子作为输出。令这个目标函数为 V:B→ R 来表示 V 把任何合法的棋局映射到某一 个实数值(用R来表示实数集合)。我们打算让这个目标函数 V 给好的棋局赋予较高的评分。
把对任务 T 提高性能 P 的问题简化为:学习象 ChooseMove 这样某个特定的目标函数。目标函数的选择是一个关键的设计问题
- 如果 b 是一最终的胜局,那么 V(b)=100
- 如果 b 是一最终的负局,那么 V(b)=-100
- 如果 b 是一最终的和局,那么 V(b)=0
- 如果 b 不是最终棋局,那么 V(b)=V(b′),其中 b′是从 b 开始双方都采取最优对弈后可达到的终局。
然而,由于这个定义的递归性,它的运算效率不高,所以这个定义对于西洋跳棋比赛者不可用,这个定义被称为不可操作的定义。 我们经常希望学习算法仅得到目标函数的某个近似(approximation),由于这个原因学习目标函数的过程常被称为函数逼近(function approximation)。使用\(\hat{V}\)来表示程序中实际学习到的函数,以区别理想目标函数 V。
假设每个棋局选择6个特征,于是令\(\hat{V}(b)\)为线性函数: $$ \hat{V}(b) = w_0 + w_1x_1+w_2x_2+w_3x_3+w_4x_4+w_5x_5+w_6x_6 $$
对于一个训练样本序偶\(< b, V_{train}(b)>\),b表示棋盘状态X,\(V_{train}(b)\)表示当前棋盘理论上的评分。
(2)对于非终局如何生成评分:使用训练值估计法则
$$ V_{train}(b)←\hat{V}ˆ{(Successor(b))} $$ 其中Successor(b)表示 b 之后再轮到程序走棋时的棋盘状态(也就是程序走了一步和对手回应一步后的棋局)
(3)进一步定义最佳拟合训练数据的含义,又叫代价函数
$$ E = \sum_{< b, V_{train}(b)> \in 训练样例}(V_{train}(b) - \hat{V}(b)) $$ 至此,我们的目标就是寻找权值,使对于观测到的训练数据 E 值最小化。
(4)选择一种优化算法:LMS 权值更新法则
$$ w_i←w_i+η(V_{train}(b)-\hat{V}(b))x_i (b)) xi $$
(5)最终设计
执行系统(Performance system),这个模块是用学会的目标函数来解决给定的任务, 在此就是对弈西洋跳棋。它把新问题(新一盘棋)的实例作为输入,产生一组解答路线(对 弈历史记录)作为输出。在这里,执行系统采用的选择下一步走法的策略是由学到的评估函 数Vˆ 来决定的。所以我们期待它的性能会随着评估函数的日益准确而提高。
鉴定器(Critic),它以对弈的路线或历史记录作为输入,输出目标函数的一系列训练样 例。如图所示,每一个训练样例对应路线中的某个棋盘状态和目标函数给这个样例的评估值 Vtrain。在我们的例子中,鉴定器对应式 1.1 给出的训练法则。
泛化器(Generalizer),它以训练样例作为输入,输出一个假设,作为它对目标函数的 估计。它从特定的训练样例中泛化,猜测一个一般函数,使其能够覆盖这些样例以及样例之 外的情形。在我们的例子中,泛化器对应 LMS 算法,输出假设是用学习到的权值 w0 ,…, w6 描述的函数Vˆ 。
实验生成器(Experiment Generator),它以当前的假设(当前学到的函数)作为输入, 输出一个新的问题(例如,最初的棋局)供执行系统去探索。它的角色是挑选新的练习问题, 以使整个系统的学习速率最大化。在我们的例子中,实验生成器采用了非常简单的策略:它 总是给出一个同样的初始棋局来开始新的一盘棋。更完善的策略可能致力于精心设计棋子位 置以探索棋盘空间的特定区域。
3、本书的一般观点
将学习问题看作搜索问题,
二、概念学习和一般到特殊序
1、概念学习介绍
给定一样例集合以及每个样例是否属于某一概念的标注,怎样自动推断出该概念的一般定义。这一问题被称为概念学习(concept learning),或称从样例中逼近布尔值函数。
定义: > 概念学习是指从有关某个布尔函数的输入输出训练样例中,推断出该布尔函数。
概念学习分类问题的一种解决方式
2、一般约定
- 概念定义在一个实例(instance)集合之上,这个集合表示为
X - 待学习的概念或函数称为目标概念 (targetconcept),记作
c - 一般来说,
c可以是定义在实例X上的任意布尔函数,即c:X→{0, 1} - 在学习目标概念时,必须提供一套训练样例(training examples)
- 每个样例为
X中的一个实例x以及它的目标概念值c(x) c(x)=1的实例被称为正例(positive example),c(x)=0的实例为反例(negative example)- 可以用序偶
<x,c(x)>来描述训练样例 - 符号
D用来表示训练样例的集合 - 使用符号
H来表示所有可能假设(all possible hypotheses)的集合 H中每个的假设h表示X上定义的布尔函数,即h:X→{0,1}- 机器学习的目标就是寻找一个假设
h,使对于X中的所有x,h(x)=c(x) - 本书的观点:将学习问题看作搜索问题
3、假设的一般到特殊序
定义符号 \≥_g\) 表示 … 比 … 更一般:
令 \(h_j\)和 \(h_k\) 为在 X 上定义的布尔函数。定义一个
... 比 ... 更一般的关系,记做\(≥_g\)。称 \(h_j≥_g h_k\) 当且仅当: $$ (\forall x \in X)[(h_k(x)=1)→(h_j(x)=1)] $$
\(≥_g\)关系很重要,因为它在假设空间 H 上对任意概念学习问题提供了一种有用的结构。后面的章节将阐述概念学习算法如何利用这一偏序结构,以有效地搜索假设空间。
4、Find-S:寻找极大特殊假设
(1)算法描述
- 将 h 初始化为 H 中最特殊假设
- 对每个正例 x
- 对 h 的每个属性约束 ai
- 如果 x 满足 ai 则
- 不做任何事
- 如果 x 不满足 ai 则
- 将 h 中 ai 替换为 x 满足的紧邻的更一般约束,泛化了
每个属性中的可取值(从一般到特殊的取值)
- 由“?”表示任意值
- 明确指定的属性值(如 AirTemp=Warm)
- 由“∅”表示不接受任何值
也就是说一步一步的将布尔函数一步一步的泛化,抽取所有样本中正类中共有的属性
问题:
- 没有考虑到负类的情况
- 没有描述不确定性的机制
- 无法处理多个特殊假设
其他略,太晦涩
三、函数近似和决策树学习
1、函数近似
(1)问题设置
- 可能的实例集合X
- 未知的目标函数 f:X->Y
- 假设函数集合 H={h|h:X->Y}
(2)输入
未知目标函数的训练样本 \({< x^{(i)}, y^{(i)} >}\)
(3)输出
最接近目标函数的假设函数 h ∈ H
(4)例子
简单的训练样本集合
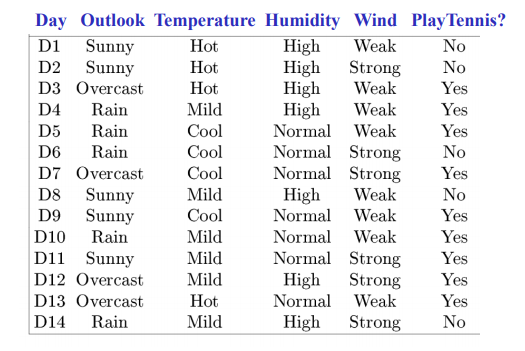
一个对于f: < Outlook, Temperature, Humidity, Wind > -> PlayTennis? 的决策树
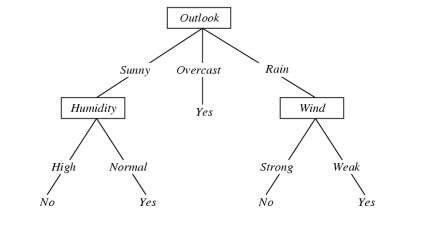
- 每一个内联节点:测试一个离散值属性Xi
- 每一个节点分支:对于Xi的一个选择
- 每一个叶子:预测值Y(或者P(Y|X ∈ leaf))
2、决策树学习
(1)描述
问题设置
- 可能的实例集合X
- 每一个实例在X中的x是一个特征向量
- 例如: < Humidity=low, Wind=weak, Outlook=rain, Temp=hot >
- 未知的目标函数 f:X->Y
- 如果在这天打网球则Y=1,否则Y=0
- 假设函数集合 H={h|h:X->Y}
- 每个假设函数 h 是一个决策树
- trees sorts x to leaf, which assigns y
输入
未知目标函数的训练样本 \({< x^{(i)}, y^{(i)} >}\)
输出
最接近目标函数的假设函数 h ∈ H
(2)决策树的顶层描述(ID3算法)
[ID3百科]https://baike.baidu.com/item/ID3%E7%AE%97%E6%B3%95/5522381 ID3算法详解 奥卡姆剃刀原理百科
如无必要,勿增实体
node = Root Main loop:
- A is the best decision attribute for next node
- Assign A as decision attribute for node
- For each value of A, create new descendant of node
- Sort training examples to leaf nodes
- if training examples perfectly classified ,then stop, else iterate over new leaf nodes
node = Root
主循环: 1.A是对于下一个节点的“最佳”决策属性,信息增益越大,越好 2.分配A作为节点的决策属性 3.对于A的每个值,创建节点的新后代 4.将训练示例分为叶节点 5.如果训练样本完全分类,然后停止,否则迭代新叶节点
(3)熵、条件熵和信息增益
熵函数是一个描述当前节点选择优劣的量度,熵函数越小越好
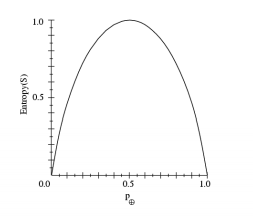
- S是一个简单的训练集
- \(p_{\oplus}\) 是样例中正类中出现的可能性
- \(p_{-}\) 是样例中负类中出现的可能性
- 熵表示S的混杂程度(不确定程度)
$$ H(S) = -p_{\oplus}\log_2{p_{\oplus}} - p_{-}\log_2{p_{-}} $$
随机变量X的熵H(X) $$ H(X) = - \sum_{i=1}^{n}P(X=i)\log_2P(X=i) $$
Mutual information (aka Information Gain) of X and Y 条件熵 $$ H(X|Y=v) = - \sum_{i=1}^{n}P(X=i|Y=v)\log_2P(X=i|Y=v) $$
Conditional entropy H(X|Y) of X given Y 条件熵 $$ H(X|Y) = - \sum_{v\in values(Y)} P(Y=v)\log_2P(X|Y=v) $$
Mutual information of X and Y (又称信息增益) $$ I(X,Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) $$
信息增益(Information Gain)是输入属性A和目标变量Y之间的相互信息
信息增益是由于对变量A的排序而导致的数据样本S的目标变量Y的熵的预期减少 $$ Gain(S,A) = I_S(A,Y) = H_S(Y) - H_S(Y|A) $$
理解
熵是代表随机变量的不确定度 条件熵代表在某一个条件下,随机变量的复杂度(不确定度) 信息增益=信息熵-条件熵,信息增益大的特征可以减少随机变量X的不确定性,即这个特征很重要。
计算信息增益例子
信息增益越大,表示这个信息很关键

代码描述
import math
def entropy(*args):
total = sum(args)
ret = 0.0
for arg in args:
ret += -(math.log(arg/total,2)*arg/total)
return ret
E = entropy(9,5)
Gain1 = E - (7/14)*entropy(3,4) - (7/14)*entropy(6,1)
Gain2 = E - (8/14)*entropy(6,2) - (6/14)*entropy(3,3)(4)一些问题
过度拟合
考虑假设函数 h 的如下问题
- Error rate over training data(?):\(error_{train}(h)\)
- True error rate over all data(?):\(error_{true}(h)\)
如果\( error_{true}(h) > error_{train}(h) \),则 假设函数h出现过拟合 过拟合的量度:\( error_{true}(h) - error_{train}(h) \)
过拟合现象
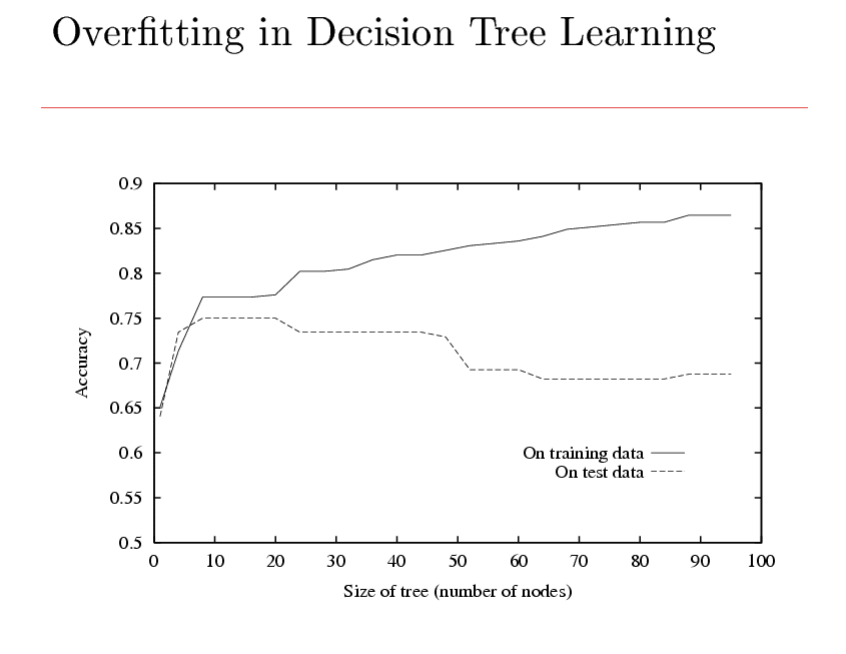
避免过拟合
- stop growing when data split not statistically significant
- grow full tree, then post-prune(剪枝)
减少错误剪枝
分割数据为训练集和验证集 创建正确的分类树 剪枝直到出现错误:
- 评估每个节点对于验证集的影响
- 贪心的删除那些最能提高验证集合节点
也就是说生成最精确的树的规模最小的决策树
错误剪枝现象
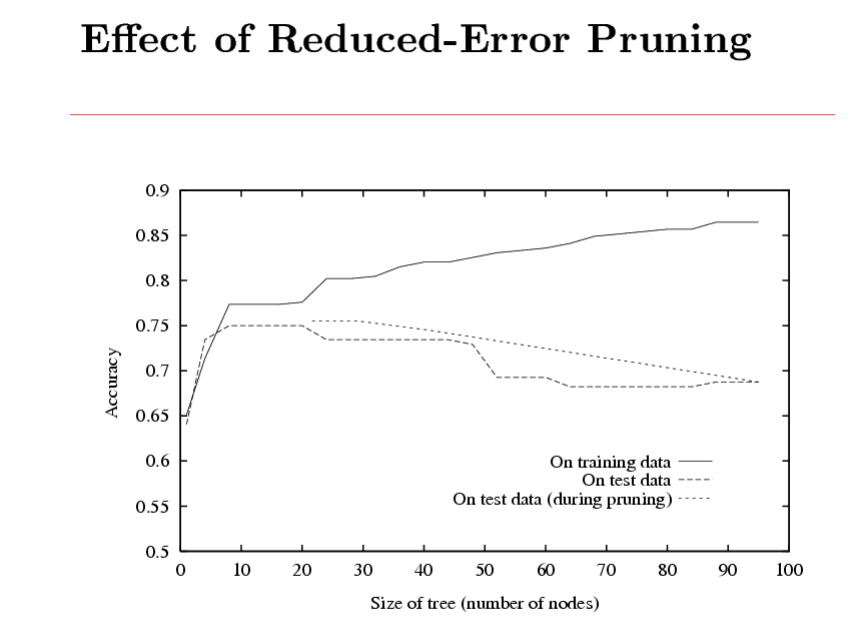
如何处理连续型的属性(非离散) 创建边界(分界值)
如何处理非二值化的离散数据 类似于二值化的
3、概率论相关知识
(1)要点
- 事件
- 离散随机变量
- 连续随机变量
- 复合事件
- 概率公理
- 什么定义了一个合理的不确定理论
- 独立事件
- 条件概率
- 贝叶斯定理
- 联合概率分布
- 期望
- 独立,有条件的独立
(2)随机变量
- 非正式地,如果A是随机变量,则:
- A表示我们不确定的东西
- 也许是随机实验的结果
- 例子
- 如果我们班上随机画的人是女性,则为A = 真
- The hometown of a randomly drawn person from our class
- 如果我们班上的两名随机抽奖的人有相同的生日,则为A = 真
- 将
P(A)定义为 A为True的可能性- 随机变量的所有可能性的集合 被定义为样本空间S
- 随机变量A是在S上定义的函数
A: S -> {0,1}
- 事件是S的一个子集
- 我们通常对特定事件和特定事件的可能性感兴趣,这些事件将以其他特定事件为条件
(3)概率公理
- 0 <= P(A) <= 1
- P(True) = 1
- P(False) = 0
- P(A or B) = P(A) + P(B) - P(A and B)
推论 P(A) = P(A and B) + P(A and ~B)
(4)条件概率的定义
P(A|B) = P(AB) / P(B) #读作:在B发生的条件下A发生的概率 变形 P(AB) = P(A|B) P(B) 链式规则 p(A^B^C) = P(A|BC) P(BC) = P(A|BC) P(B|C) P©
(5)贝叶斯规则
因为: P(AB) = P(A|B)P(B) P(AB) = P(B|A)P(A) 所以: P(A|B) = (P(B|A) P(A))/P(B)
其他形式的贝叶斯公式
$$
P(A|B) = \frac{P(B|A)P(A)}{P(B|A)P(A)+P(B|~A)P(~A)} \
P(A|BX) = \frac{P(B|AX)P(AX)}{P(BX)}
$$
(6)期望值
$$
E[X] = \sum_{x \in X} xP(X=x) \
E[f(x)] = \sum_{x \in X} f(x)P(X=x)
$$
(7)协方差
给定连个离散随机变量X、Y我们定义X和Y的协方差为: $$ Cov(X,Y) = E[(X-E[X])(Y-E[Y])] $$ 例如:X = 性别,Y = 踢足球